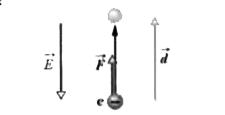
Electrons are continually being knocked out of air molecules in the atmosphere by cosmic-ray particles coming in from space. Once released, each electron experiences an electric force $\to F$ due to the electric field $\to E$ that is produced in the atmosphere by charged particles already on Earth. Near Earth's surface the electric field has the magnitude $E = 150 N / C$ and is directed downward. What is the change $Δ U$ in the electric potential energy of a released electron when the electric force causes it to move vertically upward through a distance $d = 520$ m (Fig. 24-4)? Through what potential change does the electron move?

Text Solution

Verified by Experts

(1) The change $Δ U$ in the electric potential energy of the electron is related to the work W done on the electron by the electric field. Equation $24 - 5 (W = - Δ U)$ gives the relation. (2) The work done by a constant force $\to F$ on a particle undergoing a displacement $\to d$ is
$w = \to F . \to d .$
(3) The electric force and the electric field are related by the force equation $\to F = q \to E$ , where here q is the charge of an electron $(= - 1.6 \times 10^{- 19} C) .$
Calculations: Substituting the force equation into the work equation and taking the dot product yield
$W = q \to E . \to d = q E d cos θ$ .
where $θ$ is the angle between the directions of $\to E and - \to d .$ .The field $\to E$ is directed downward and the displacement $\to d$ is directed upward, so $θ = 180^{\circ}$ . We can now evaluate the work as
$W = (- 1.6 \times 10^{- 19} C (150 N / C) (520 m) {cos 180}^{\circ}$
$= 1.2 \times 10^{- 14}$ J.
Equation 24-5 then yields
$Δ U = - W = - 1.2 \times 10^{- 14}$ (Answer)
This result tells us that during the 520 m ascent, the electric potential energy of the electron decreases by $1.2 \times 10^{- 14}$ J. To find the change in electric potential, we apply Eq. $24 - 4$ :
$Δ V = \frac{Δ U}{- q} = \frac{- 1.2 \times 10^{- 14} J}{- 1.6 \times 10^{- 19} C}$
$= 7.5 \times 10^{4} V = 75 k V$ . (Answer)
This tells us that the electric force does work to move the electron to a higher potential.

Updated on:21/07/2023

Due to the earth's magnetic field, charged cosmic ray particles
ACan nevar reach the pole
BCan never reach the equator
CRequired greeter kinetic energy to reach the equalor than pole
DRequir less kinetic energy to reach the equator than pole
Due to the earth's magnetic field, charged cosmic ray particles
ARequire greater kinetic energy to reach the equatorthan the poles
Bto reach the equator than the poles
CCan never reach the equator
DCan never reach the poles
a proton placed in an electric field would experience an electrical force equal to its weight. the magnitude of electric field intensity E would be
A $m^{2} \frac{g}{e}$
B $e^{2} \frac{m^{2}}{g}$
Cmg/e
De/mg