A ball of mass of 1 kg and charge 50μC is directly projected from infinity toward another fixed ball of charge 1/6μC ( as shown in Fig. 24-5). The initial velocity of projection is 10 m/s. Find the distance and its velocity at the closest separation. Assume that the initial line of motion is at a distance of 1 m from the second fixed charge.
To solve the problem, we need to analyze the motion of the charged ball as it approaches the fixed charged ball. We will use the principles of energy conservation and electrostatic force.
Given Data:
- Mass of the moving ball, m=1kg
- Charge of the moving ball, q1=50μC=50×10−6C
- Charge of the fixed ball, q2=16μC=16×10−6C
- Initial velocity of the moving ball, v0=10m/s
- Initial distance from the fixed charge, r0=1m
Step 1: Calculate the initial kinetic energy (KE) of the moving ball.
The kinetic energy is given by the formula:
KE=12mv2
Substituting the values:
KE=12×1×(10)2=12×1×100=50J
Step 2: Calculate the initial potential energy (PE) at a distance of 1 m from the fixed charge.
The potential energy between two point charges is given by:
PE=k⋅|q1⋅q2|r
where k=8.99×109N m2/C2.
Substituting the values:
PE=8.99×109⋅|50×10−6⋅16×10−6|1
Calculating the charge product:
|q1⋅q2|=50×10−6⋅16×10−6=506×10−12=8.33×10−12C2
Now substituting back into the potential energy equation:
PE=8.99×109⋅8.33×10−121≈0.0748J
Step 3: Apply the conservation of energy principle.
At the closest approach, all kinetic energy will be converted into potential energy. Therefore:
KEinitial+PEinitial=KEfinal+PEfinal
At the closest approach, the kinetic energy will be zero, and we can denote the closest distance as r:
50+0.0748=0+k⋅|q1⋅q2|r
50.0748=8.99×109⋅8.33×10−12r
Step 4: Solve for r.
Rearranging the equation gives:
r=8.99×109⋅8.33×10−1250.0748
Calculating r:
r≈0.074850.0748≈0.00149m≈1.49mm
Step 5: Calculate the velocity at the closest separation.
Using conservation of energy again:
KEinitial+PEinitial=KEfinal+PEfinal
At the closest separation, we can find the final kinetic energy:
KEfinal=KEinitial+PEinitial−PEfinal
Substituting the values:
KEfinal=50+0.0748−8.99×109⋅8.33×10−120.00149
Calculating PEfinal at r:
PEfinal≈0.0748J
Thus,
KEfinal≈50−0.0748≈49.9252J
Now, using KE=12mv2:
49.9252=12×1×v2
v2=99.8504⇒v≈9.99m/s
Final Results:
- Closest distance: r≈1.49mm
- Velocity at closest separation: v≈9.99m/s
- Mass of the moving ball, m=1kg
- Charge of the moving ball, q1=50μC=50×10−6C
- Charge of the fixed ball, q2=16μC=16×10−6C
- Initial velocity of the moving ball, v0=10m/s
- Initial distance from the fixed charge, r0=1m
The kinetic energy is given by the formula:
KE=12mv2
Substituting the values:
KE=12×1×(10)2=12×1×100=50J
The potential energy between two point charges is given by:
PE=k⋅|q1⋅q2|r
where k=8.99×109N m2/C2.
PE=8.99×109⋅|50×10−6⋅16×10−6|1
Calculating the charge product:
|q1⋅q2|=50×10−6⋅16×10−6=506×10−12=8.33×10−12C2
Now substituting back into the potential energy equation:
PE=8.99×109⋅8.33×10−121≈0.0748J
At the closest approach, all kinetic energy will be converted into potential energy. Therefore:
KEinitial+PEinitial=KEfinal+PEfinal
At the closest approach, the kinetic energy will be zero, and we can denote the closest distance as r:
50+0.0748=0+k⋅|q1⋅q2|r
50.0748=8.99×109⋅8.33×10−12r
Rearranging the equation gives:
r=8.99×109⋅8.33×10−1250.0748
Calculating r:
r≈0.074850.0748≈0.00149m≈1.49mm
Using conservation of energy again:
KEinitial+PEinitial=KEfinal+PEfinal
At the closest separation, we can find the final kinetic energy:
KEfinal=KEinitial+PEinitial−PEfinal
Substituting the values:
KEfinal=50+0.0748−8.99×109⋅8.33×10−120.00149
Calculating PEfinal at r:
PEfinal≈0.0748J
Thus,
KEfinal≈50−0.0748≈49.9252J
Now, using KE=12mv2:
49.9252=12×1×v2
v2=99.8504⇒v≈9.99m/s
- Closest distance: r≈1.49mm
- Velocity at closest separation: v≈9.99m/s
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.03 Locating equipotential surfaces1videos
ELECTRIC POTENTIAL
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.04 Finding the potential change from the electric field1videos
ELECTRIC POTENTIAL
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type1videos
ELECTRIC POTENTIAL
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Integer Type )3videos
ELECTRIC CHARGES AND FIELDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Integer Type)14videos
ELECTROMAGNETIC INDUCTION
Similar Questions
A particle of mass 1kg and charge 1/3μC is projected toward a nonconducing fixed spherical shell of radius r=1mm having the same charge uniformly distributed on its surface. Find th minimum initial velocity of projection requires if the particle just grazes the shell.
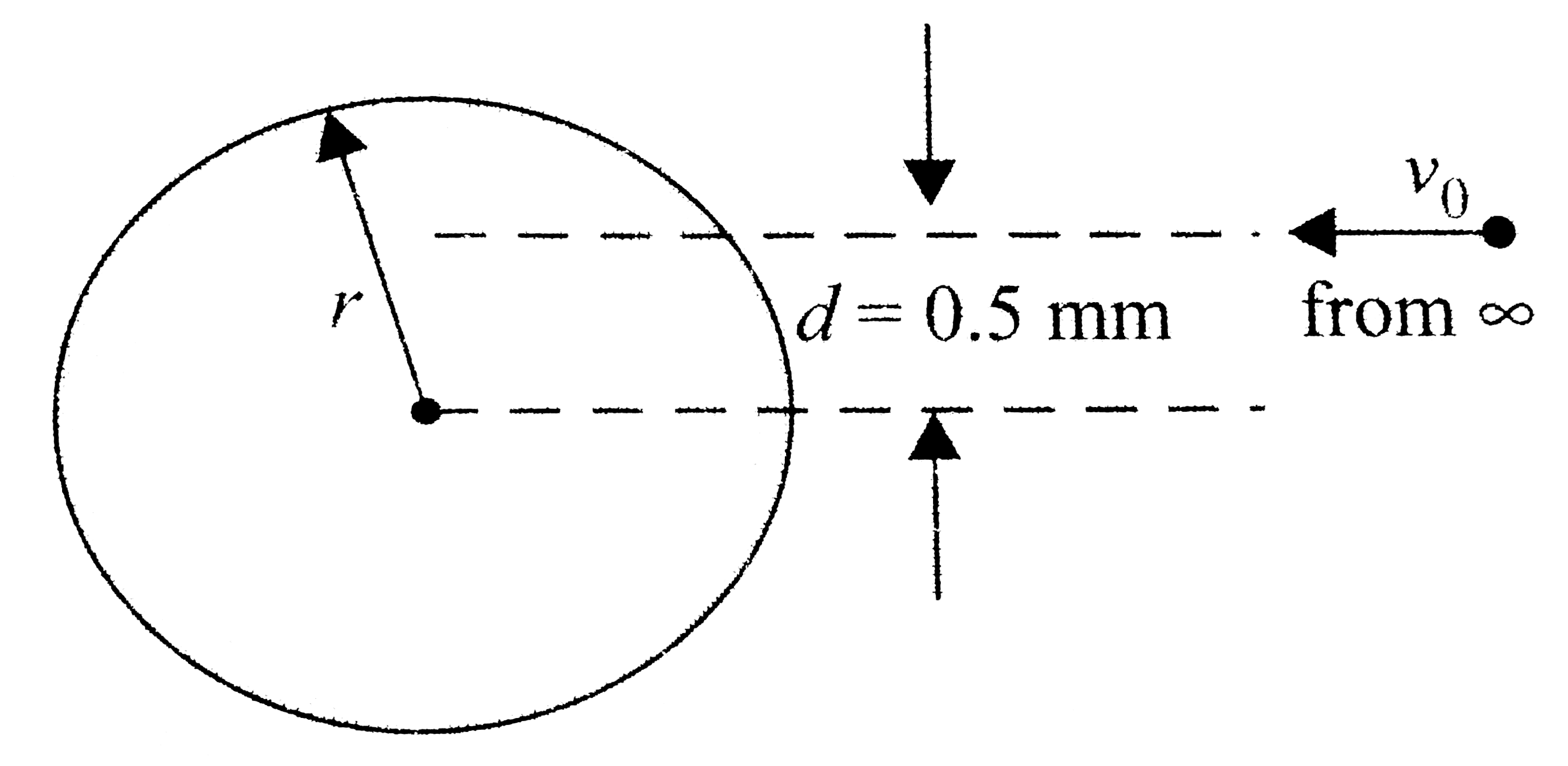 .View Solution
.View SolutionAssume that a point charge q is projected from a large distance toward the center of a fixed charged ring along its axis. What should be its initial velocity so that the charge may reach the other side of infinity?
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass 2 g and charge 1μC is held at rest on a frictionless surface at a distance of 1m from a fixed charge of 1 mC. If the particle is released it will be repelled. The speed of the particle when it is at distance of 10 m from fixed charge is :
A100 m/sB90 m/sC60 m/sD45 m/s - Question 2 - Select One
A ball is projected with a velocity of 20m/s vertically. Find the distance travelled in first three second. (use g=10m/sec2 )
A20mB25mC30mD50m - Question 3 - Select One
In the diagram shown the charge +Q is fixed. Another charge +2q and mass M is projected from a distance R from the fixed charge. Minimum separtion between the two charge if the velocity becomes 1√3 time of the projected velocity, at this moment is (Assume gravity to be absent)
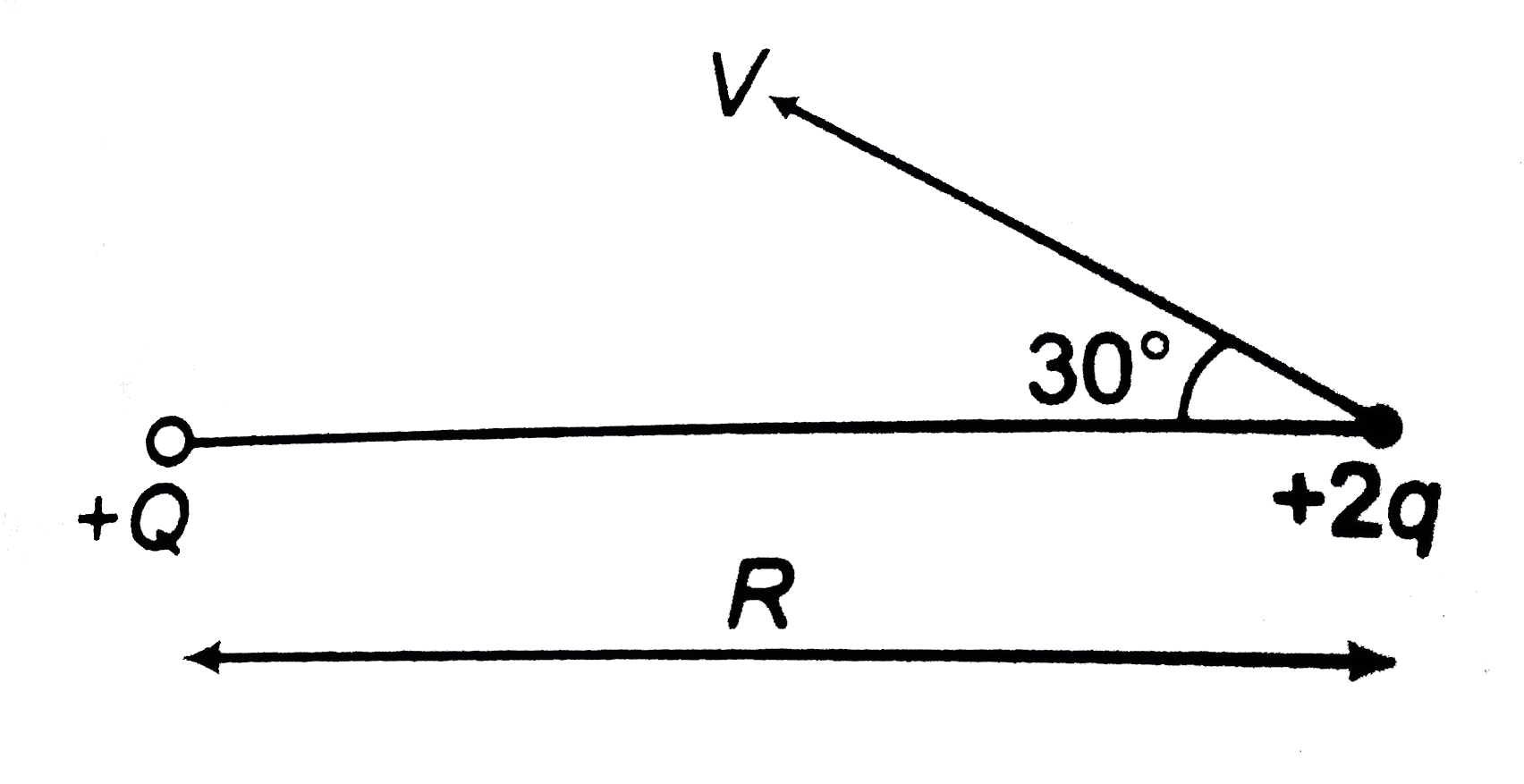 A√32RB1√3RC12RDnone of these
A√32RB1√3RC12RDnone of these
A positive charge +Q is fixed at a poibt A. Another positively charged particle of mass m and charge +q is projected from a point B with velocity u as shown in (Fig. 3.103). Point B is at a large distance from A and at distance d from the line A C. The initial velocity is parallel to the line A C. The point C is at a very large distance from A. Find the minimum distance (in meter) of +q from +Q during the motion. Take Qq=4πε0mu2d and d(√2−1)m.
 .View Solution
.View SolutionA particle of mass 100 gm and charge 2μC is released from a distance of 50 cm from a fixed charge of 5μC. Find the speed of the particle when its distance from the fixed charge becomes 3 m.
View SolutionA particle of mass 100 gm and charge 2μC is released from a distance of 50 cm from a fixed charge of 5μC. Find the speed of the particle when its distance from the fixed charge becomes 3 m.
View SolutionA charged particle of mass m and charge q is kept initially at rest on a frictionless surface. Another charged particle of mass 4m and charge 2q starts moving with velocity v towards it. Calculate the distance of the closest approach for both the charged particles.
View SolutionWith what velocity a ball be projected vertically so that the distance covered by it in 5th second is twice the distance it covers in its 6th second (g=10m/s2)
View Solution

