(a) Figure 24-10a shows two points i and fin a uniform electric field →E. The points lie on the same electric field line (not shown) and are separated by a distanced. Find the potential difference Vf−Vi by moving a positive test charge q0 from i to f along the path shown, which is parallel to the field direction.
(b) Now find the potential difference Vf−Vi by moving the positive test charge q0 from i to f along the path icf shown in Fig. 24-10b.
We can find the potential difference between any two points in an electric field by integrating →E.d→s along a path connecting those two points according to Eq. 24-20.
Calculations: We have actually already done the calculation for such a path in the direction of an electric field line in a uniform field when we derived Eq. 24-23. With slight changes in notation, Eq. 24-23 gives us
Vf−Vi=−Ed. (Answer)
Calculations: The Key Idea of (a) applies here too, except now we move the test charge along a path that consists of two lines: is and cf. .At all points along line is, the displacement d→s of the test charge is perpendicular to →E. Thus, the angle θ between →Eandd→s is 90°, and the dot product →E.d→s is 0. Equation 24-20 then tells us that points i and c are at the same potential: Vc−Vi=0. Ah, we should have seen this coming. The points are on the same equipotential surface, which is perpendicular to the electric field lines.
For lines cf we have θ=45∘ and, from Eq 24−20,
Vf−Vi−∫fc→E.d→s=−∫fcE(cos45∘)ds
=−E(cos45∘)∫fcds.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.05 Finding electric potential
1 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.06 Finding the potential
1 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.03 Locating equipotential surfaces
1 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Integer Type )
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Integer Type)
14 Videos
Similar Questions
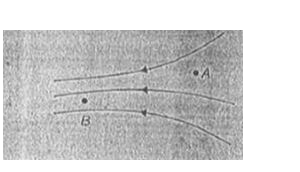
In figure two points A and B are located in a region of electric field . The potential difference VB−VA is
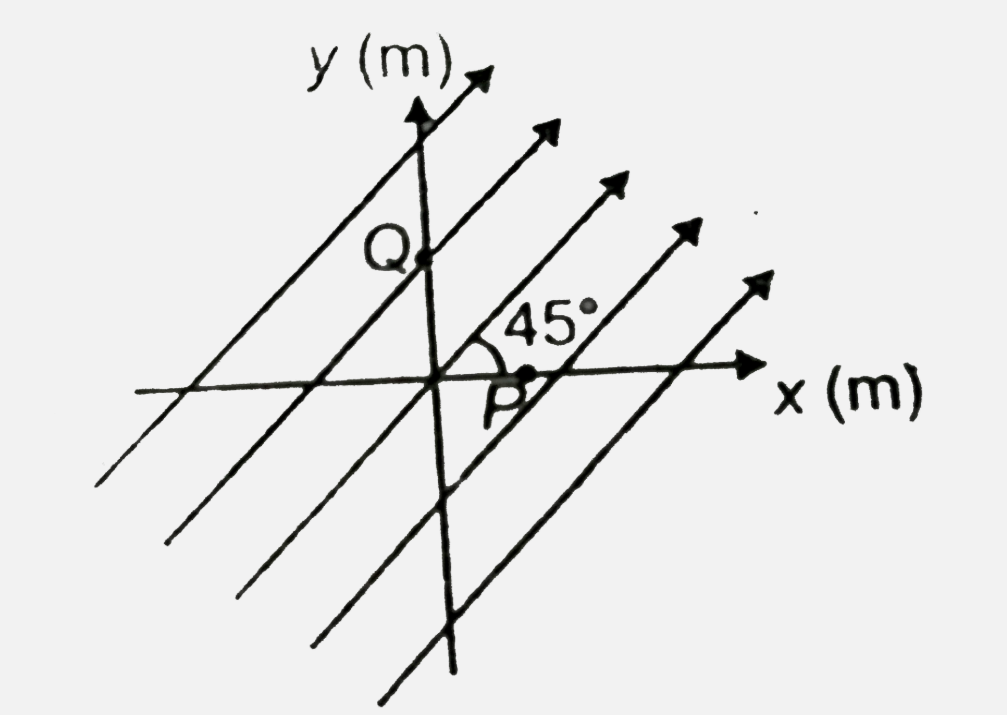
View SolutionA uniform electric field of 200 V / m is directed at 45∘ with x -axis as shown in figure. The co-ordinates of point P and point Q are (1,0) and ( 0,2) . Find the potential difference , VP−VQ ( in volts) .
View Solution
Knowledge Check
In figure two points A and B are located in a region of electric field . The potential difference VB−VA is
 APositiveBNegativeCZeroDNone of these
APositiveBNegativeCZeroDNone of theseA uniform electric field of 400Vm is directed at 45∘ above the x-axis as shown in the figure. The potential difference VA−VB is given by
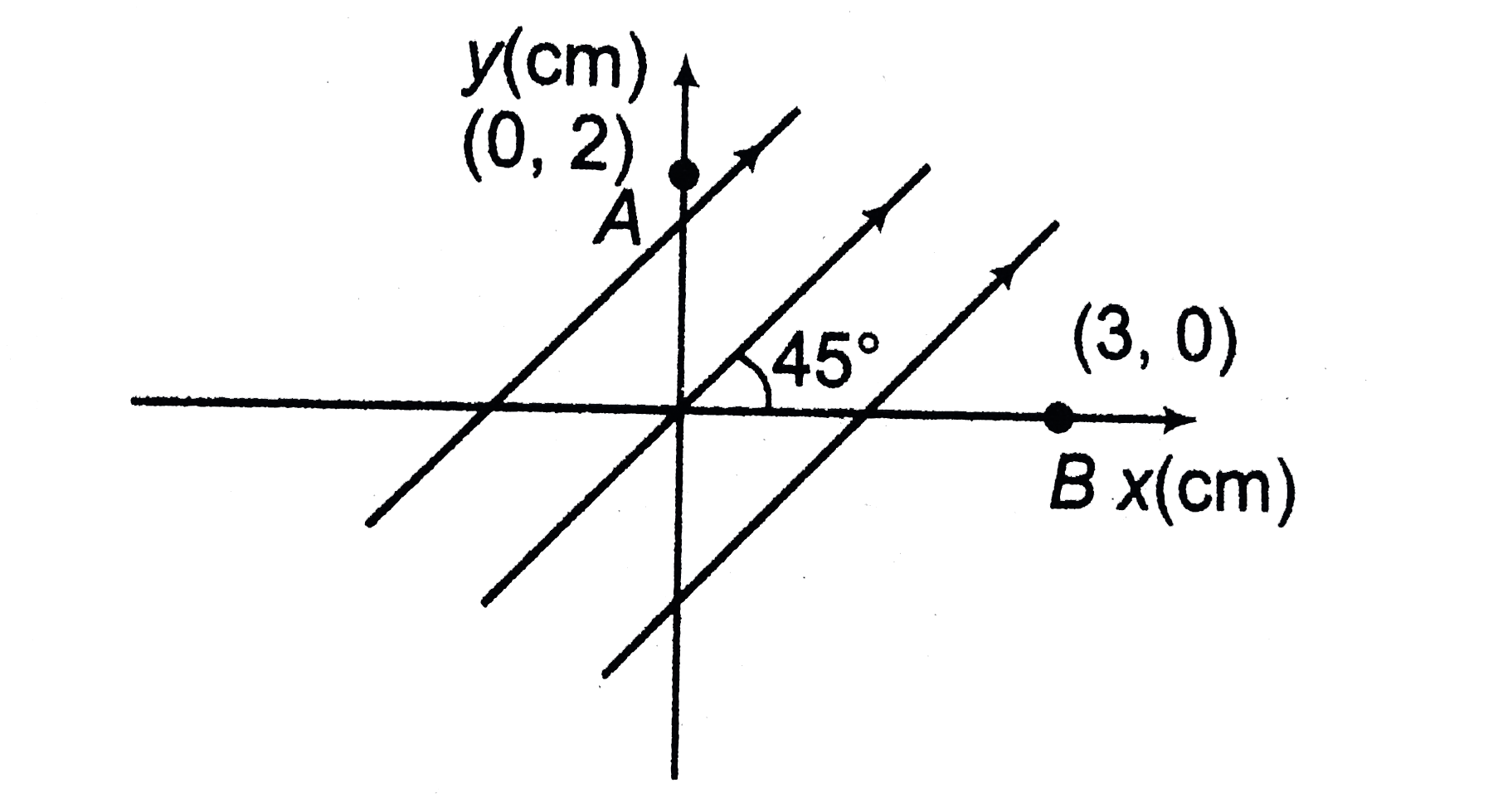 A0B4VC6.4VD2.8V
A0B4VC6.4VD2.8V
A uniform electric field of 200 V / m is directed at 45∘ with x -axis as shown in figure. The co-ordinates of point P and point Q are (1,0) and ( 0,2) . Find the potential difference , VP−VQ ( in volts) .

View SolutionThree points A,B,C lie in a uniform electric field E of 5×103N/C as shown in Fig. Find the potential difference between A and C.

View SolutionA uniform electric field of 400Vm is directed at 45∘ above the x-axis as shown in the figure. The potential difference VA−VB is given by
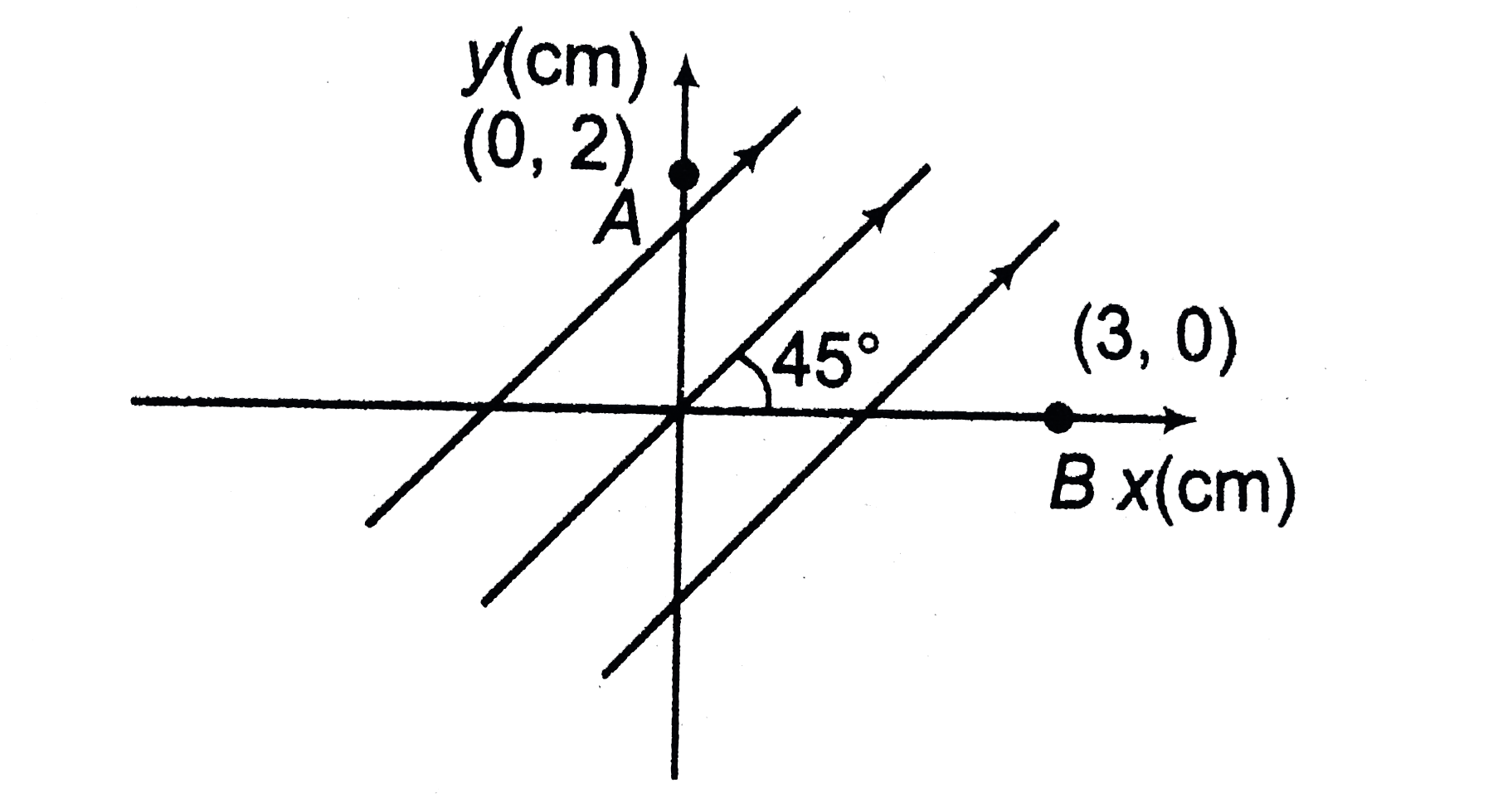
View Solution‘A point charge +Q is placed at point O as shown in the figure. Is the potential difference VA–VB positive.
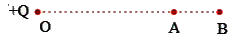
View SolutionFigure shows two rings having charges Q and −√5Q. Find potential difference a and B i.e. (VA−VB).
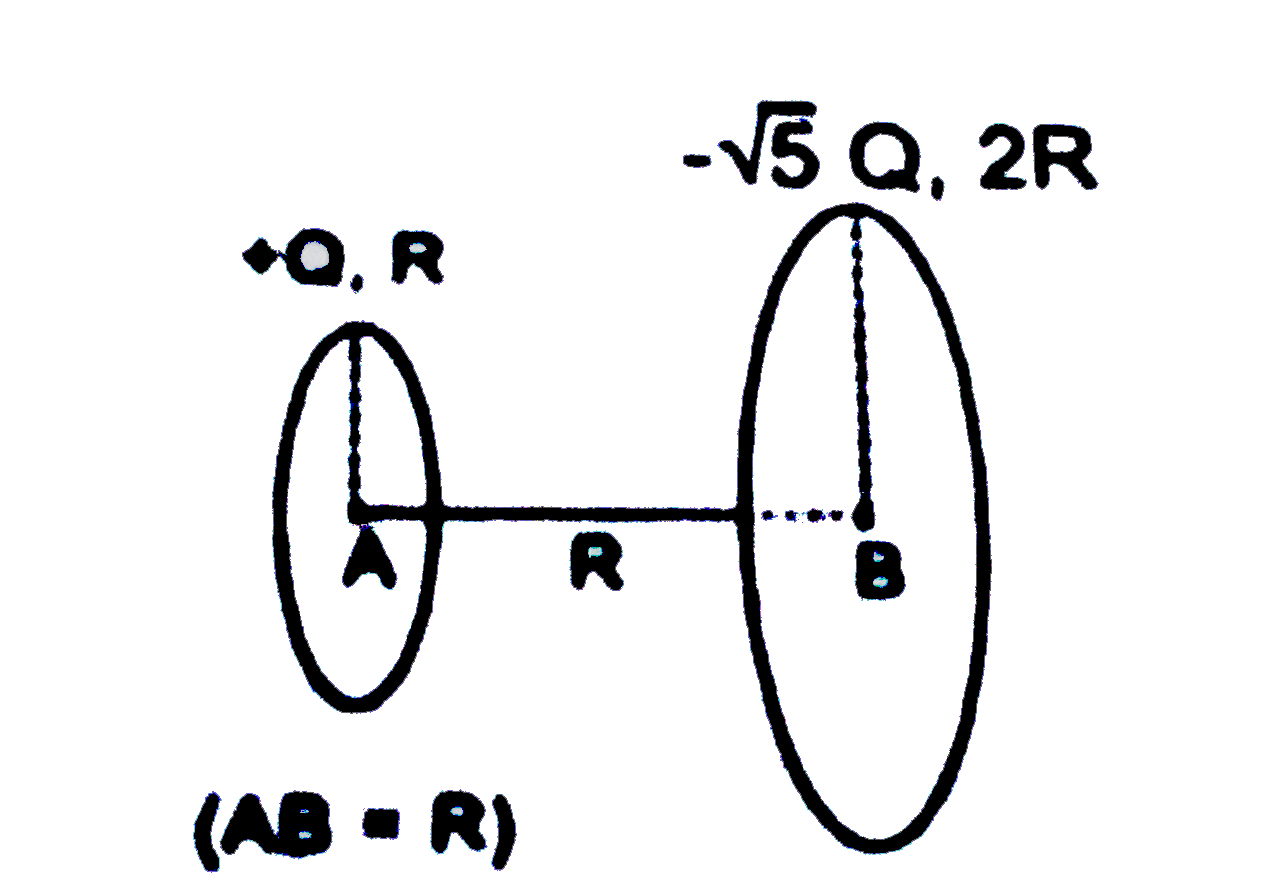
View SolutionFigure shows two rings having charges Q and −√5Q. Find potential difference a and B i.e. (VA−VB).
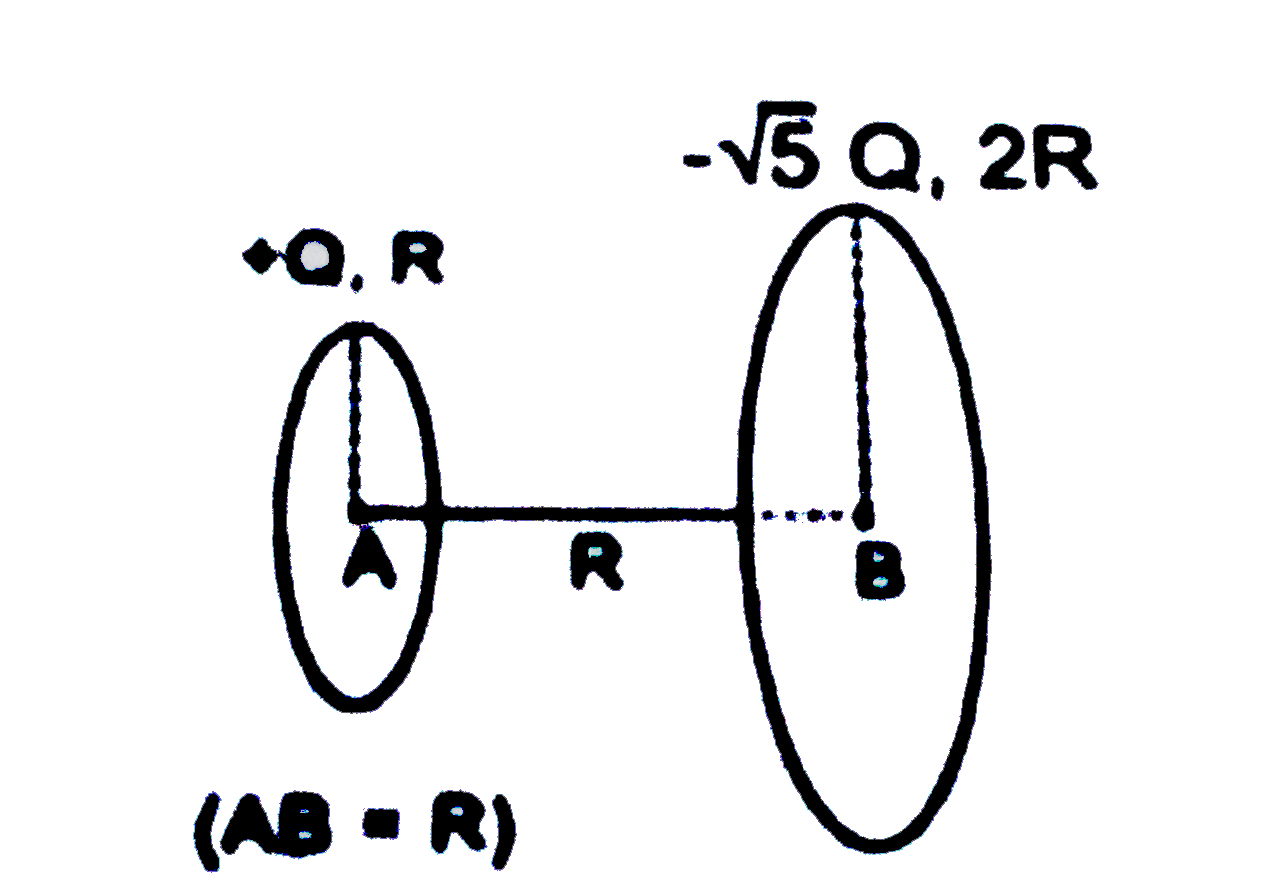
View Solution
