Assume that a point charge q is projected from a large distance toward the center of a fixed charged ring along its axis. What should be its initial velocity so that the charge may reach the other side of infinity?
To solve the problem of determining the initial velocity required for a point charge q to reach the other side of infinity when projected toward the center of a fixed charged ring, we can follow these steps:
Step 1: Understand the System
We have a fixed charged ring with charge Q and radius A. A point charge q is projected from a large distance (infinity) towards the center of the ring along its axis.
Step 2: Identify the Forces and Energy Conservation
Since the charge q is projected towards the ring, we need to consider the forces acting on it. The ring exerts an electric force on the charge q. To find the initial velocity needed, we will use the principle of conservation of energy.
Step 3: Set Up the Energy Conservation Equation
The total mechanical energy at infinity (where the potential energy is zero and the kinetic energy is given by the initial velocity) must equal the total mechanical energy at the center of the ring (where we want the charge to momentarily stop).
The conservation of energy can be expressed as:
Potential Energy at Infinity+Kinetic Energy at Infinity=Potential Energy at Center+Kinetic Energy at Center
At infinity:
- Potential Energy U∞=0
- Kinetic Energy K∞=12mv2 (where v is the initial velocity)
At the center of the ring (point O):
- Potential Energy UO=kQqA (where k is Coulomb's constant)
- Kinetic Energy KO=0 (since we want the charge to stop at the center)
Step 4: Write the Energy Equation
Substituting the values into the energy conservation equation gives:
0+12mv2=kQqA+0
Step 5: Solve for Initial Velocity
Rearranging the equation to solve for v:
12mv2=kQqA
Multiply both sides by 2:
mv2=2kQqA
Now, divide both sides by m:
v2=2kQqmA
Taking the square root gives us the initial velocity:
v=√2kQqmA
Final Answer
The initial velocity v required for the charge q to reach the other side of infinity is:
v=√2kQqmA
---
We have a fixed charged ring with charge Q and radius A. A point charge q is projected from a large distance (infinity) towards the center of the ring along its axis.
Since the charge q is projected towards the ring, we need to consider the forces acting on it. The ring exerts an electric force on the charge q. To find the initial velocity needed, we will use the principle of conservation of energy.
The total mechanical energy at infinity (where the potential energy is zero and the kinetic energy is given by the initial velocity) must equal the total mechanical energy at the center of the ring (where we want the charge to momentarily stop).
- Potential Energy U∞=0
- Kinetic Energy K∞=12mv2 (where v is the initial velocity)
- Potential Energy UO=kQqA (where k is Coulomb's constant)
- Kinetic Energy KO=0 (since we want the charge to stop at the center)
Substituting the values into the energy conservation equation gives:
Rearranging the equation to solve for v:
The initial velocity v required for the charge q to reach the other side of infinity is:
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.16 Finding the field from the potential1videos
ELECTRIC POTENTIAL
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.17 Acceleration of charge of given potential1videos
ELECTRIC POTENTIAL
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - SAMPLE PROBLEM 24.14 Field and potential inside a charged spherical shell1videos
ELECTRIC POTENTIAL
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Integer Type )3videos
ELECTRIC CHARGES AND FIELDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Integer Type)14videos
ELECTROMAGNETIC INDUCTION
Similar Questions
A particle of mass m and charge +q approaches from a very large distance towards a uniformly charged ring ofradius Rand charge, mass same as that of particle, with initial velocity v0 along the axis of the ring as shown in the figure-1.420. What is the closest distance of approach between the ring and the particle? Assume the space to be gravity free and frictionless :
 View Solution
View SolutionCalculate distance of the point from the centre of a uniformly charged ring on its axis, where it electric field intensity becomes maximum.
View Solution
Knowledge Check
- Question 1 - Select One
A point charge +q is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of plane is
Adirected perpendicular to the plane away from the planeBdirected perpendicular to the plane but towards the planeCdirected radially away from the point chargeDdirected radially towards the point charge - Question 2 - Select One
Two identical coaxial rings each of radius R are separated by a distance of √3R. They are uniformly charged with charges +Q and −Q respectively. The minimum kinetic energy with which a charged particle (charge +q) should be projected from the centre of the negatively charged ring along the axis of the rings such that it reaches the centre of the positively charged ring is
AQq4πε0RBQq2πε0R)CQq8πε0RD3Qq4πε0R - Question 3 - Select One
An electron released on the axis of a positively charged ring at a large distance from the centre will
ANot moveBDo oscillatory motionCDo SHMDDo non-periodic motion
A point charge of charge -q and mass m is released with negligible speed from a distance √3R on the axis of a fixed uniformly charged ring of charge Q and radius R. Find out its velocity when it reaches it reaches at the centre of the ring.
 View Solution
View SolutionA conducting spherical shell of outer radius R and inner radius r = 3R/4 has no net charge on it. At its center there is a point charge q, and at a distance 2R from its center there is a point charge Q (Fig.) . (a) What is the magnitude of the electrostatic force on the charge q at the center due to the shell ? (b) What is the magnitude of net force on it?
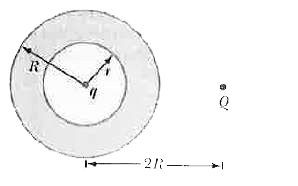 View Solution
View SolutionTwo concentric rings placed in a gravity free region in yz-plane one of radius R carries a+Q and second of radius 4R and charge –8Q distributed uniformly over it. Find the velocity with which a point charge of mass m and charge +q should be projected from a a distance 3R from the centre of rings on its axis so that it will reach to the centre of the rings.
View SolutionTwo fixed charges are as shown. Where should the third charge be placed so that its in equilibrium?
 View Solution
View SolutionA point charge +q, is placed at a distance d from an isolated conducting plane. The field at a point P on the other side of the plane is
View Solution

