In Fig.32-30 a light ray in water is incident at angle θ1 on a boundary with an underlying material into which some of the light refracts . There are two choices of underlying material. For each the angle of refreaction θ2 versus the incident angle θ1 is given in Fig. 32-30b . The vertical axis scale is set by θ2s=90∘ . Without calculation determine whether the index of refraction of (a) material 1 and (b) material 2 is greater or less than the index of water (n=1.33) . What is the index of refraction of (c) material 1 and (d) material 2?
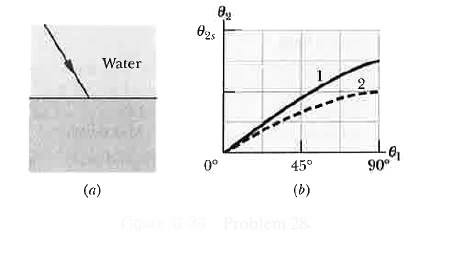
(a) n2>n1 , (b) the value of n2 for material 2 is also greater than that oif water (n1) (c ) n2 = 1.4 for material 1 , (d) n2 = 1.9
Topper's Solved these Questions
- ELECTROMAGNETIC WAVES BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type )
62 Videos
- ELECTROMAGNETIC WAVES BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type )
4 Videos
- ELECTROMAGNETIC WAVES BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - CHECKPOINT
3 Videos
- ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT EXERCISE - Practice Questions (Integer)
7 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (Integer Type )
5 Videos
Similar Questions
A ray of light falls on a material body at an incident angle 60∘ and refracted at angle 30∘.
What is the refractive index of the material?
View SolutionA ray of light falls on a material body at an incident angle of 30∘ and refracted at angle 60∘.
What is the refractive index of the material?
View Solution
Knowledge Check
When light travels from glass to air, the incident angle is θ1 and the refracted angle is θ2. The true relation is
Aθ1=θ(2)Bθ1<θ2Cθ1>θ2DNot predictableA ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of the prism is 5∘ and the prism is made of a material of refractive index 1.5, the angle of incidence is.
A7.5∘B5∘C15∘D2.5∘A ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of prism is 5∘ and the prism is made of a material of refractive index 1.5, the angle of incidence is
A7.5∘B5∘C15∘D2.5∘
When light travels from glass to air, the incident angle is θ1 and the refracted angle is θ2. The true relation is
View SolutionA ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of the prism is 5∘ and the prism is made of a material of refractive index 1.5, the angle of incidence is.
View SolutionA ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of the prism is 5∘ and the prism is made of a material of refractive index 1.5, the angle of incidence is.
View SolutionA ray of light is incident on a prism of refracting angle A. if θC is the critical angle for the material of the prism with respect to the surrounding air, then:
View SolutionA ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of the prism is 5∘ and the prism is made of a material of refractive index 1.5, the angle of incidence is.
View Solution
