A convex lens of focal length 40 cm is held coaxially 12 cm above a mirror of focal length 18 cm. An object held x cm above the lens gives rise to an image coincident with it. Then x is equal to:

12 cm
15 cm
18 cm
30 cm
The correct Answer is:B
u=24cm,v=x
Using 1v−1u=1f
or1x−124=140
∴ x=15cm

Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - DISHA PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Exercise - 1 : Concept Builder (Topicwise)(Topic 4 : Prism and Dispersion of Light)
9 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - DISHA PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Exercise - 1 : Concept Builder (Topicwise)(Topic 5 : Optical Instruments)
5 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - DISHA PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Exercise - 1 : Concept Builder (Topicwise)(Topic 2 : Refraction of Light at Plane Surface and Total Internal Reflection)
17 Videos
- PHYSICAL WORLD, UNITS AND MEASUREMENTSBOOK - DISHA PUBLICATIONCHAPTER - PHYSICAL WORLD, UNITS AND MEASUREMENTSEXERCISE - Exercise - 2 : Concept Applicator
30 Videos
- SEMICONDUCTOR ELECTRONICS : METERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - DISHA PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS : METERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - EXERCISE -2: CONCEPT APPLICATOR
25 Videos
Similar Questions
A convex lens of focal length 40cm is held at a distance 12cm coaxially above a concave mirror of focale length 18cm.
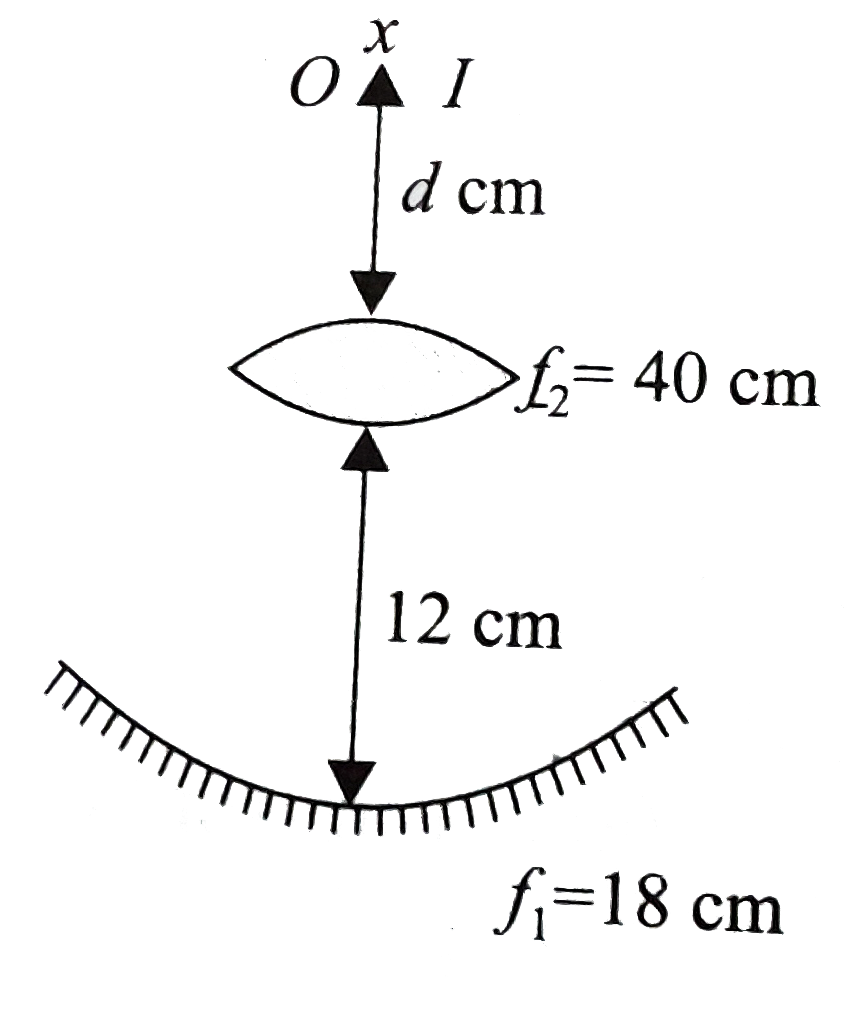
Q. A luminous point object placed d cm above the lens on its axis gives rise to an imag coincident iwth itself, then the value of d is equal to
View SolutionOne side of radius of curvature R2=120cm of a convexo-convex lens of material of refractive index μ=1.5 and focal length f1=40cm is slivered. It is placed on a horizontal surface with silvered surface in contact with it. Another convex lens of focal length f2=20cm is fixed coaxially d=10cm above the first lens. A luminous point object O on the axis gives rise to an image coincide with it. Find its height above the upper lens.
View Solution
Knowledge Check
A convex lens of focal length 40cm is held at a distance 12cm coaxially above a concave mirror of focale length 18cm.

Q. A luminous point object placed d cm above the lens on its axis gives rise to an imag coincident iwth itself, then the value of d is equal toA15cmB30cmC24cmD18cmA convex lens of focal length 40 cm is in contact with a concave lens of focal length 25 cm. The power of the combination is
A−1.5dioptersB−6.5 dioptersC+6.5 dioptersD+6.67 dioptersA convex lens of focal length 40cm is in contact with a concave lens of focal length 25cm. The power of the combination is
A−1.5 dioptresB−6.5 dioptresC+6.5 dioptresD+6.67 dioptres
One side of radius of curvature R2=120cm of a convexo-convex lens of material of refractive index μ=1.5 and focal length f1=40cm is slivered. It is placed on a horizontal surface with silvered surface in contact with it. Another convex lens of focal length f2=20cm is fixed coaxially d=10cm above the first lens. A luminous point object O on the axis gives rise to an image coincide with it. Find its height above the upper lens.
View SolutionA convex lens of focal length 40 cm is in contact with a concave lens of focal length 25 cm. The power of the combination is
View SolutionA convex lens of focal length 40cm is held at a distance 12cm coaxially above a concave mirror of focale length 18cm.
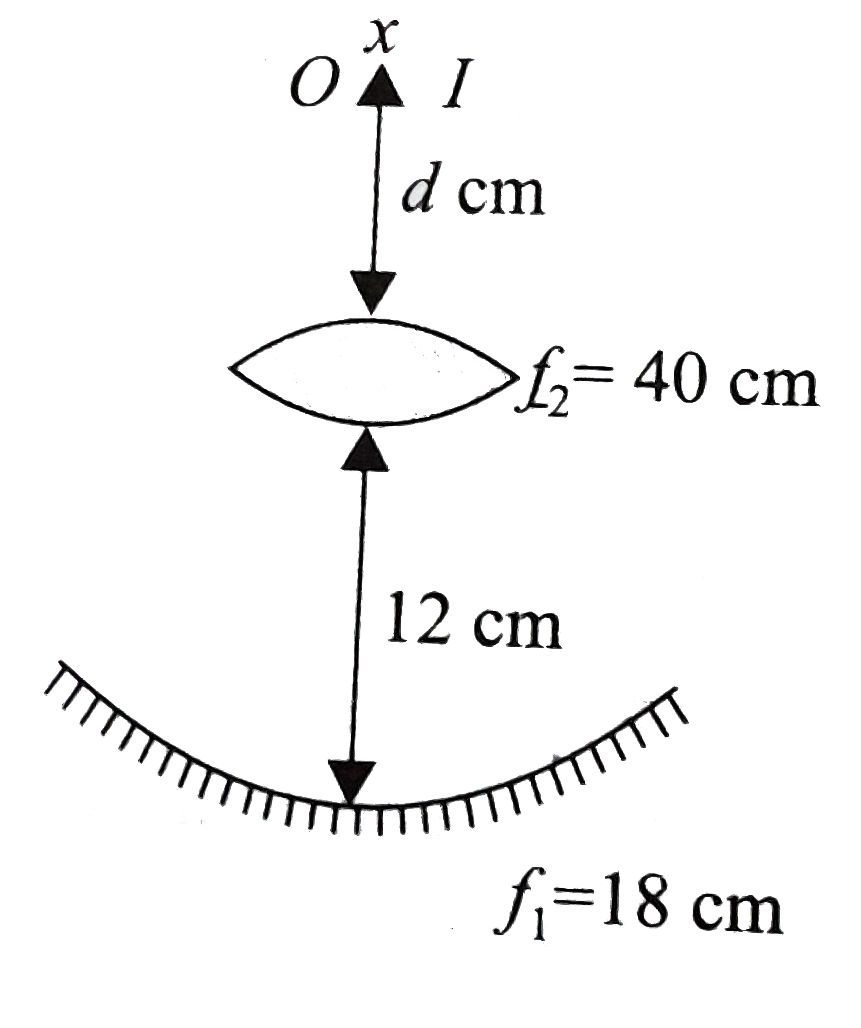
Q. If the convex lens is replaced by a concave lens of focal llength 60cm, it gives rise to an image coincident with itself. then the value of d is
View SolutionA convex lens of focal length 40 cm is in contact with a concave lens of foal length 25 cm. The power of the lens combination is
View SolutionA convex lens of focal length 40cm is held at a distance 12cm coaxially above a concave mirror of focale length 18cm.
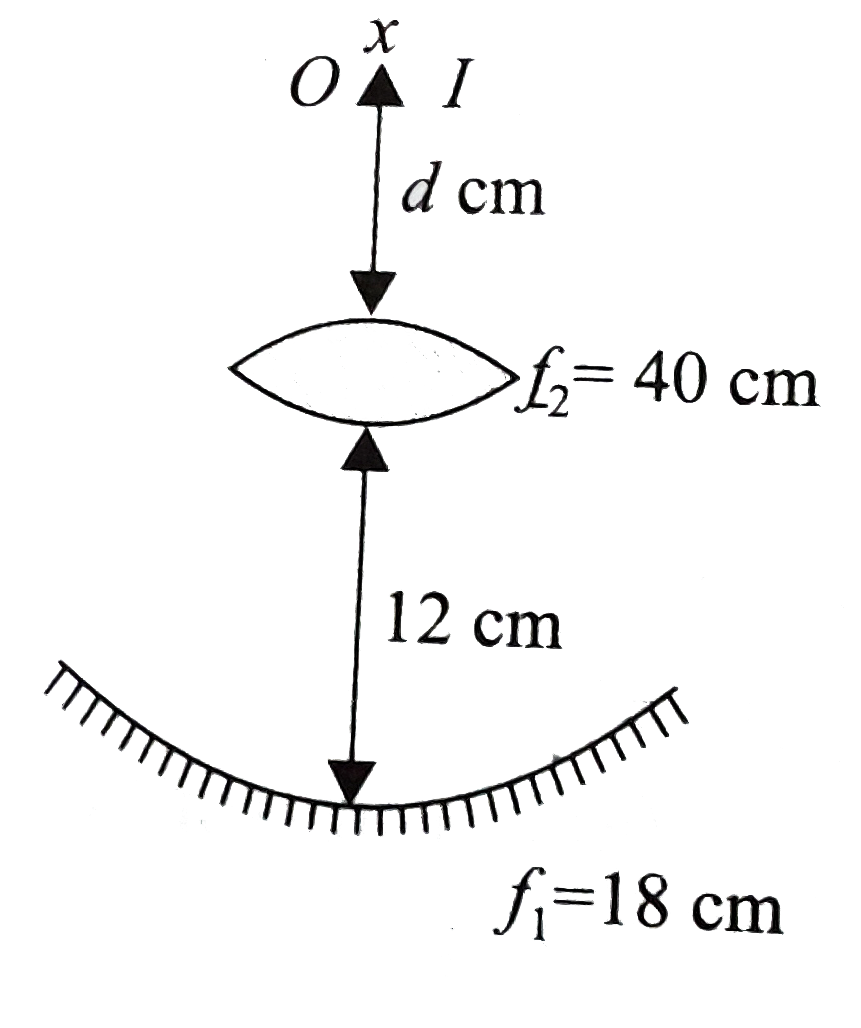
Q. If the convex lens is replaced by a glass plate of thickness 6cm, refractive index μ=32 and gives rise to an image coincident with itself, then the value of d is equal to
View Solution
