ABCD is a cyclic quadrilateral. AB and DC are produced to meet at P. If ∠ADC=70degreeand∠DAB=60degree, then the ∠PBC+∠PCB is
130∘
150∘
155∘
180∘
The correct Answer is:A
To solve the problem, we will use the properties of cyclic quadrilaterals and the angles formed by the intersection of lines.
1. Understanding the Cyclic Quadrilateral:
- A cyclic quadrilateral is a quadrilateral whose vertices lie on a circle. The opposite angles of a cyclic quadrilateral are supplementary.
2. Given Angles:
- We are given that ∠ADC=70∘ and ∠DAB=60∘.
3. Finding Angle ABC:
- In a cyclic quadrilateral, the angle opposite to ∠ADC is ∠ABC.
- Therefore, ∠ABC=180∘−∠ADC=180∘−70∘=110∘.
4. Finding Angle DAB:
- We already have ∠DAB=60∘.
5. Finding Angles PBC and PCB:
- The angles ∠PBC and ∠PCB are the angles formed at point P by the lines AB and DC.
- By the exterior angle theorem, we know that:
∠PBC+∠PCB=∠DAB+∠ADC
- Substitute the values:
∠PBC+∠PCB=60∘+70∘=130∘
6. Final Answer:
- Therefore, ∠PBC+∠PCB=130∘.
Conclusion:
The value of ∠PBC+∠PCB is 130∘.
- A cyclic quadrilateral is a quadrilateral whose vertices lie on a circle. The opposite angles of a cyclic quadrilateral are supplementary.
- We are given that ∠ADC=70∘ and ∠DAB=60∘.
- In a cyclic quadrilateral, the angle opposite to ∠ADC is ∠ABC.
- Therefore, ∠ABC=180∘−∠ADC=180∘−70∘=110∘.
- We already have ∠DAB=60∘.
- The angles ∠PBC and ∠PCB are the angles formed at point P by the lines AB and DC.
- By the exterior angle theorem, we know that:
∠PBC+∠PCB=∠DAB+∠ADC
- Substitute the values:
∠PBC+∠PCB=60∘+70∘=130∘
- Therefore, ∠PBC+∠PCB=130∘.
The value of ∠PBC+∠PCB is 130∘.
Similar Questions
ABCD is a cyclic quadrilateral in which sides AD and BC are produced to meet at P, and sides DC and AB meet at Q when produced. If ∠A=60∘ and ∠ABC=72∘ then ∠DPC−∠BQC=
ABCD एक चक्रीय चतुर्भुज है जिसमें भुजाओं AD तथा BC को बढ़ाया जाता है जो P पर मिलती हैं तथा भुजाओं DC और AB को बढ़ाया जाता है जो Q पर मिलती हैं | यदि ∠A=60∘ तथा ∠ABC=72∘ है, तो ∠DPC−∠BQC= ?
View SolutionABCD is a cyclic quadrilateral. AB and CD when produced meet at P, if PA = 8 cm, PB = 6 cm, PC = 4 cm, then the length (in cm) of PD is.
View Solution
Knowledge Check
ABCD is a cyclic quadrilateral. AB and DC are produced to meet at P. If ∠ADC=70∘ and ∠DAB=60∘, then the ∠PBC+∠PCB is
A130∘B150∘C155∘D180∘ABCD is a cyclic quadrilateral. Diagonals AC and BD meets at P. If ∠APB=110∘ and ∠CBD=30∘, then ∠ADB measures
A55∘B30∘C70∘D80∘ABCD is a cyclic quadrilateral whose diagonals intersect at P. If AB=BC,∠DBC=70∘and∠BAC=30∘, then the measure of ∠PCD is:
Aa) 50∘Bb) 35∘Cc) 55∘Dd) 30∘
In the given figure, ABCD is a cyclic quadrilateral and diagonals D bisect each other at P. If ∠DBC=60∘and∠BAC=30∘, then ∠BCD is:
View SolutionABCD is a cyclic quadrilateral in which sides AD and BC are produced to meet at P, and sides DC and AB meet at Q when produced. If ∠A=60∘ and ∠ABC=72∘ then ∠DPC−∠BQC=
ABCD एक चक्रीय चतुर्भुज है जिसमें भुजाओं AD तथा BC को बढ़ाया जाता है जो P पर मिलती हैं तथा भुजाओं DC और AB को बढ़ाया जाता है जो Q पर मिलती हैं | यदि ∠A=60∘ तथा ∠ABC=72∘ है, तो ∠DPC−∠BQC= ?
View SolutionSides AB and DC of a cyclic quadrilateral ABCD are produced to meet at E, and sides AD and BC are produced to meet at F. If ∠ADC=75∘ and ∠BEC=52∘, then the difference between ∠BAD and ∠AFB ? /
एक चक्रीय चतुर्भुज ABCD की भुजाओं AB और DC को बढ़ाया जाता है जो E पर मिलती हैं तथा भुजाओं AD और BC को बढ़ाया जाता है जो F पर मिलती हैं | यदि ∠ADC=75∘ तथा ∠BEC=52∘ हैं, तो ∠BAD तथा ∠AFB के बीच क्या अंतर है?
View SolutionA dog takes 3 leaps for every 5 leaps of a hare. If one leap of the dog is equal to 3 leaps of the hare, the ratio of the speed of the dog to that of the hare is :
View SolutionThe sides AB and CD of a cyclic quadrilateral ABCD are produced to meet at P. The sides AD and BC are produced to meet at Q. If ∠ADC=85∘and∠BPC=40∘, then ∠BAD is equal to
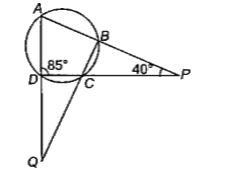
View Solution
