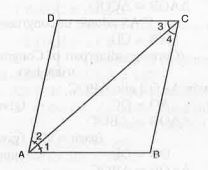
ABCD is a parallelogram. CE bisects ∠C and AF bisects ∠A. In each of the following, if the statement is true, give a reason for the same. (a) ∠A=∠C
Step by step video & image solution for ABCD is a parallelogram. CE bisects /_C and AF bisects /_A. In each of the following, if the statement is true, give a reason for the same. (a) /_A=/_C by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Similar Questions
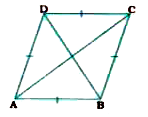
ABCD is a rhombus. Show that diagonal AC bisects ∠Aas well as ∠Cand diagonal BD bisects ∠Bas well as ∠D.
View SolutionIn Figure, ABCD is a parallelogram, CE besects ∠C and AF bisects ∠A. In each of the following, if the statement is true, give a reason for the same: ∠A=∠C (ii) ∠FAB=12∠A (iii)∠DCE=12∠C
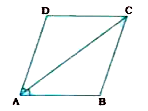
View SolutionDiagonal AC of a parallelogram ABCD bisects ∠A (see the given figure), show that :
it bisects ∠C also,
View SolutionABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D .
View SolutionIn parallelogram ABCD, ∠A−∠B=30∘ Then ∠C=………
View SolutionDiagonal AC of a parallelogram ABCD bisects ∠A (See fig.)
 . Show that It bisects ∠C also.
. Show that It bisects ∠C also.
View SolutionABCD is a rhombus. Show that the diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.
View SolutionIf in rectangle ABCD
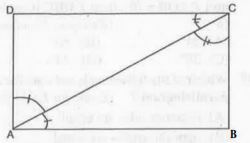 , diagonal AC bisects ∠A as well as ∠C , then ABCD is a :
, diagonal AC bisects ∠A as well as ∠C , then ABCD is a :
View Solution
