Explain how this figure is a trapezium. Which of its two sides are parallel? (Fig 3.32)
To explain how the given figure is a trapezium and identify its parallel sides, we can follow these steps:
1. Definition of a Trapezium:
A trapezium (or trapezoid) is defined as a quadrilateral that has at least one pair of parallel sides.
2. Identify the Figure:
Let's consider the figure mentioned in the question (Fig 3.32). We need to analyze the sides of this quadrilateral.
3. Examine the Sides:
In the figure, we will denote the vertices of the trapezium as K,L,M,N. We need to check the lengths and angles of the sides KL,LM,MN, and NK.
4. Check for Parallelism:
To determine if two sides are parallel, we can look for equal angles or use the properties of parallel lines. In this case, we observe that side MN is parallel to side KL. This can be established by showing that the angles formed with a transversal line are equal.
5. Conclusion:
Since we have identified that sides KL and MN are parallel, we can conclude that the figure is a trapezium. Therefore, the two sides that are parallel are KL and MN.
Final Statement:
Thus, the figure is a trapezium because it has one pair of parallel sides, specifically KL and MN.
---
A trapezium (or trapezoid) is defined as a quadrilateral that has at least one pair of parallel sides.
Let's consider the figure mentioned in the question (Fig 3.32). We need to analyze the sides of this quadrilateral.
In the figure, we will denote the vertices of the trapezium as K,L,M,N. We need to check the lengths and angles of the sides KL,LM,MN, and NK.
To determine if two sides are parallel, we can look for equal angles or use the properties of parallel lines. In this case, we observe that side MN is parallel to side KL. This can be established by showing that the angles formed with a transversal line are equal.
Since we have identified that sides KL and MN are parallel, we can conclude that the figure is a trapezium. Therefore, the two sides that are parallel are KL and MN.
Thus, the figure is a trapezium because it has one pair of parallel sides, specifically KL and MN.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.12videos
UNDERSTANDING QUADRILATERALS
- BOOK - NCERTCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.26videos
UNDERSTANDING QUADRILATERALS
- BOOK - NCERTCHAPTER - SQUARES AND SQUARE ROOTSEXERCISE - EXERCISE 6.19videos
SQUARES AND SQUARE ROOTS
- BOOK - NCERTCHAPTER - VISUALISING SOLID SHAPESEXERCISE - EXERCISE 10.38videos
VISUALISING SOLID SHAPES
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure , ABCD is a trapezium in which the parallel sides AB,CD are both perpendicular to BC. Find the area of the trapezium :
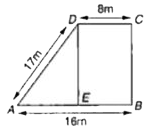 A140m2B168m2C180m2D156.4m2
A140m2B168m2C180m2D156.4m2 - Question 2 - Select One
An isosceles trapezium whose parallel sides are in the ratio 1:4. . If the sum of the two parallel sides is 70 cm,and perpendicular distance between them is 12 cm find the area of trapezium.
A616 cmB420cmC140 cmDnone of these - Question 3 - Select One
PASSAGE-II : The area of trapezium equals half the sum of parallel sides multiplied by its height.
The altitude of a trapezium when, the sum of the lengths of whose parallel sides is 6.5 cm and whose area is 26 cm2 isA20 mB4 cmC6 cmD8 cm
A circle is inscribed in a trapezium in which one of the non-parallel sides is perpendicular to the two parallel sides. Then A) the diameter of the inscribed circle is the geometric mean of the lengths of the parallel sides B) the diameter of the inscribed circle is the harmonic mean of the lengths of the parallel sides C) the area of the trapezium is the area of the rectangle having lengths of its sides as the lengths of the parallel sides of the trapezium D) the area of the trapezium is half the area of the rectangle having lengths of its sides as the lengths of the parallel sides of the trapezium
View SolutionThe opposite sides of a trapezium are parallel.
View SolutionThe lengths of the parallel sides of a trapezium are in the ratio 5:3 and the distance between them is 12 . 5 cm .If the area of the trapezium is 450cm2 , find the lengths of its parallel sides .
View SolutionThe parallel sides of a trapezium are 25cm and 13cm; its nonparallel sides are equal, each being 10cm, find the area of the trapezium.
View SolutionIf the perimeter of a trapezium be 52cm, its non parallel sides are equal to 10cm each and its altitude is 8cm, find the area of the trapezium.
View Solution

