Given a parallelogram ABCD. Complete each statement along with the definition or property used. (i) AD= (ii) <DCB= (iii) OC= (iv) m<DAB+m<CDA
To solve the question regarding the properties of the parallelogram ABCD, we will complete each statement step by step.
Solution Steps:
1. (i) AD=
Answer: BC
Reason: In a parallelogram, opposite sides are equal. Therefore, AD=BC.
2. (ii) ∠DCB=
Answer: ∠DAB
Reason: In a parallelogram, opposite angles are equal. Hence, ∠DCB=∠DAB.
3. (iii) OC=
Answer: OA
Reason: The diagonals of a parallelogram bisect each other. Therefore, OC=OA.
4. (iv) m∠DAB+m∠CDA=
Answer: 180∘
Reason: In a parallelogram, consecutive angles are supplementary. Thus, m∠DAB+m∠CDA=180∘.
Answer: BC
Reason: In a parallelogram, opposite sides are equal. Therefore, AD=BC.
Answer: ∠DAB
Reason: In a parallelogram, opposite angles are equal. Hence, ∠DCB=∠DAB.
Answer: OA
Reason: The diagonals of a parallelogram bisect each other. Therefore, OC=OA.
Answer: 180∘
Reason: In a parallelogram, consecutive angles are supplementary. Thus, m∠DAB+m∠CDA=180∘.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.12videos
UNDERSTANDING QUADRILATERALS
- BOOK - NCERTCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.26videos
UNDERSTANDING QUADRILATERALS
- BOOK - NCERTCHAPTER - SQUARES AND SQUARE ROOTSEXERCISE - EXERCISE 6.19videos
SQUARES AND SQUARE ROOTS
- BOOK - NCERTCHAPTER - VISUALISING SOLID SHAPESEXERCISE - EXERCISE 10.38videos
VISUALISING SOLID SHAPES
Similar Questions
Knowledge Check
- Question 1 - Select One
In given parallelogram ABCD values of x and y are equal to
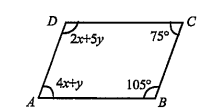 Ax=25∘,y=12.5∘Bx=12.5∘,y=25∘Cx=15∘,y=30∘Dx=15∘,y=15∘
Ax=25∘,y=12.5∘Bx=12.5∘,y=25∘Cx=15∘,y=30∘Dx=15∘,y=15∘ - Question 2 - Select One
In a parallelogram ABCD, the bisector of anl≥A also bisects BC at E, find the AD.
AABB2ABC3ABD12AB
In a parallelogram ABCD, prove that it is a rhombus, if diagonals bisect each other at 90∘
View Solution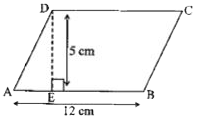
What is the area of the parallelogram ABCD as shown in the given figure?View SolutionGiven a parallelogram ABCD. If ∣∣∣−−→AB∣∣∣=a,∣∣∣−−→AD∣∣∣=b&∣∣∣−−→AC∣∣∣=c , then −−→DB.−−→AB has the value
View SolutionIn the given figure ABCD is a parallelogram, then which of the following statement is correct?
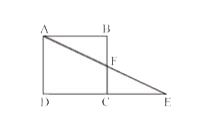 View Solution
View SolutionP is the mid-point of side AB of parallelogram ABCD. A line drawn from B parallel to PD meets CD at Q and AD produce at R. Prove that :
(i) AR = 2BC (ii) BR= 2BQView SolutionP is the mid-point of side AB of a parallelogram ABCD . A Line through B parallel to PD meets DC at Q and AD produced at R . Prove that (i) AR=2BC (ii) BR=2BQ.
View Solution


