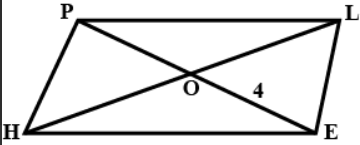
: In Fig 3.31 HELP is a parallelogram. (Lengths are in cms). Given that
OE = 4 and HL is 5 more than PE? Find OH
ABCD isaconvexquadrilateral
made of two triangles ∆ABC and ∆ADC. We know thatthe sum of the angles of a
triangle is 180 degree. So:
∠6+∠5+∠4=180∘(sum of anglesof△ABC=180∘
∠1+∠2+∠3=180∘(sum oftheangles of △ADC=180∘
addingweget
∠6+∠5+∠4+∠1+∠2+∠3
=180∘+180∘
=360
Using the angle sum propertyoftriangle, again ABCD is a
concave quadrilateral,madeoftwo△ABDand△BCD .
Therefore, the sum of all theinterioranglesofthis
quadrilateral will also be
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.26videos
UNDERSTANDING QUADRILATERALS
- BOOK - NCERTCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.311videos
UNDERSTANDING QUADRILATERALS
- BOOK - NCERTCHAPTER - SQUARES AND SQUARE ROOTSEXERCISE - EXERCISE 6.19videos
SQUARES AND SQUARE ROOTS
- BOOK - NCERTCHAPTER - VISUALISING SOLID SHAPESEXERCISE - EXERCISE 10.38videos
VISUALISING SOLID SHAPES
Similar Questions
: In Fig 3.31 HELP is a parallelogram. (Lengths are in cms). Given that OE = 4 and HL is 5 more than PE? Find OH
 View Solution
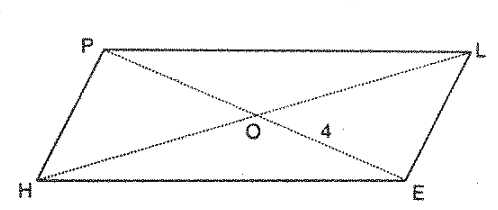
View SolutionIn Figure, HELP is a parallelogram. If OE=4cm and HL is 5cm more then PE. Find OH.
 View Solution
View SolutionConstruct a parallelogram HOME with HO = 6 cm, HE = 4 cm and OE = 3 cm.
View SolutionFind the area of a parallelogram whose base is 8cm and altitude is 4.5cm
View SolutionFind the area of a parallelogram whose base is 8.5 cm and height 4 cm .
View SolutionIn Fig.42, ABCD is a parallelogram in which AD=21 cm, DH=18 cm and DK=27 cm. The length of side AB is 63 cm (b) 63.5 cm 31.5 cm (d) 31 cm
View SolutionFind the area of a parallelogram with base 5 cm and altitude 4.2 cm.
View SolutionFind the area of a parallelogram with base 8 cm and altitude 4.5 cm.
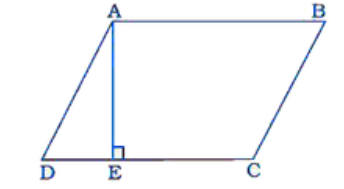
View SolutionIn Fig. 9.10, ABCD is a parallelogram, in which AB = 8 cm, AD = 6 cm and altitude AE = 4 cm. Find the altitude corresponding to side AD.
 View Solution
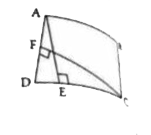
View SolutionIn the given figure ABCD is a parallelogram, AE⊥DCandCF⊥AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm then find the length of AD.
 View Solution
View Solution

