TP and TQ are any two tangents to a parabola and the tangent at a third point R cuts them in P' and Q'. Prove that TP'TP+TQ'TQ=1
Step by step video & image solution for TP and TQ are any two tangents to a parabola and the tangent at a third point R cuts them in P' and Q'. Prove that (TP')/(TP)+(TQ')/(TQ)=1 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
TP and TQ are the tangents to a circle, with centre O. Find x.
 A15∘B60∘C30∘D45∘
A15∘B60∘C30∘D45∘If TP and TQ are two tangents to a circle with centre O, so that ∠POQ=120∘, then ∠PTQ is equal to
A120∘B30∘C60∘D90∘TP and TQ are tangents from T to the circle with centre O. Then is it possible to draw a circle through the points P, O, Q and T ?
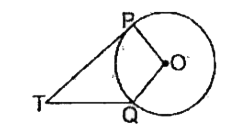 ANoBYesCCannot sayDData insufficient
ANoBYesCCannot sayDData insufficient
If TPandTQ are the two tangents to a circle with centre O. so that ∠POQ=115∘, then ∠PTQ=……….(65∘).
View SolutionTwo parallel tangents of a circle meet a third tangent at points P and Q. Prove that PQ subtends a right angle at the centre.
View SolutionIf TP and TQ are the two tangents to a circle with centre O so that ∠POQ=110∘, then ∠PTQ is equal to
View SolutionTwo tangents TP and TQ are drawn to a circle with centre O from an external point T . Prove that ∠PTQ=2∠OPQ .
View SolutionTP&TQ are tangents to the parabola, y2=4ax at P and Q. If the chord passes through the point (−a,b) then the locus of T is
View Solution
