[" For a closed surface "],[" the flux associated is "phi],[" .On adding "75 mu C" to it,"],[" it becomes "4^(phi)." Find "],[" out initial charge "],[" enclosed by surface "]
Step by step video & image solution for [" For a closed surface "],[" the flux associated is "phi],[" .On adding "75 mu C" to it,"],[" it becomes "4^(phi)." Find "],[" out initial charge "],[" enclosed by surface "] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
Answer questions on the basis of your understanding of the following paragraph and the related studied concept.
Electric flux, in general , through any surface is defined as per relation:
ϕE=∫→E.→ds , where integration has to be performed over the entire surface through which flux is required. The surface under consideration may be a closed one or an open surface. When flux through a closed surface is required we use a small circular sign on the integration symbol. Thus flux over a closed surface ∮E=∮→E.→ds. it is customary to take the outward normal as positive in this case.
A German physicist Gauss established a fundamental law to find electric flux over a closed surface. As per Gauss' law , the flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by ∈0.Mathematically ∮→E.→ds=1∈0[qen] , where qcn is the net charge enclosed within the surface. It is possible to derive Gauss' law from Coulomb's laws. Gauss' law can be applied to obtain electric field at a point due to continuous charge distribution for a number of symmetric charge configurations.
What is the electrical flux through a cube of side 'a' if a point charge 'q' is placed at one of its vertices?Aq∈0B2q∈0Cq8∈0Dq∈0.6a2 - Question 2 - Select One
20μC charge is placed inside a closed surface then flux related to surface is ϕ. If 80μC charge is added inside the surface then charge in flux is :-
A4ϕB5ϕCϕD8ϕ - Question 3 - Select One
Assertion : If a dipole is enclosed by a surface, then according to Gauss's law, electric flux linked with it will be zero.
Reason : The charge enclosed by a surface is zero.AIf both Assertion and Reason are correct and Reason is the correct explanation of AssertionBIf both Assertion and Reason are correct but Reason is not the correct explanation of AssertionCIf Assertion is true but Reason is falseDIf Assertion is false but Reason is true
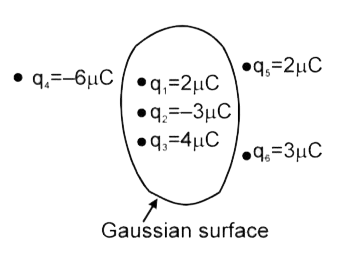
Find out flux through the given Gaussian surface.
 View Solution
View Solution5x105 lines of electric flux are entering in a closed surface and 4x105 liner come out of the surface the charge enclosed by the surface is-
View Solution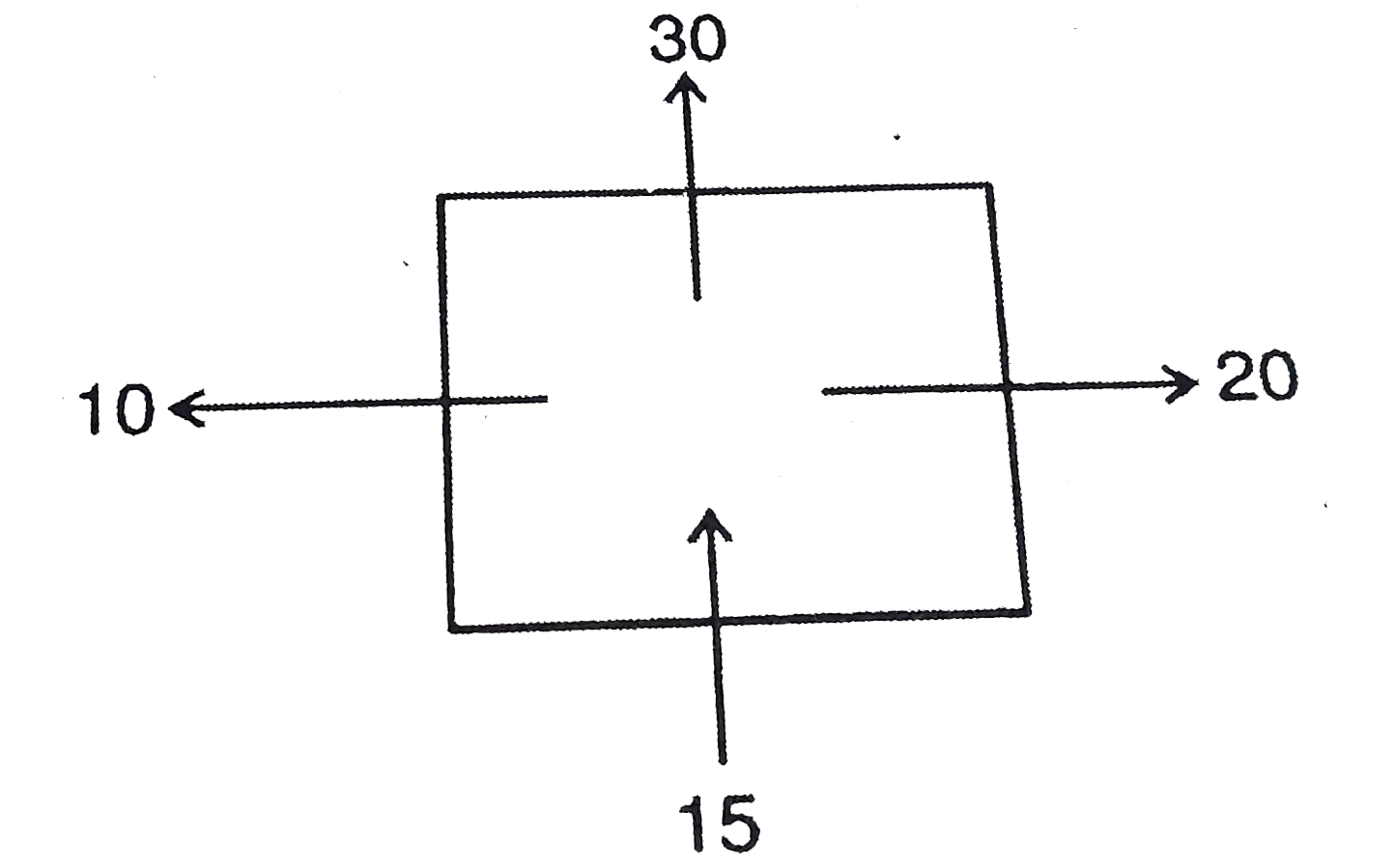
Flux (in S.I. units) coming out and eantering a closed surface is shown in the figure. Find change enclosed by the closed surface.View SolutionThe total electric flux ϕ through the entire area of a closed surface is given by
View SolutionA : If electric flux over a closed surface is negative then the surface encloses net negative charge.
R : Electric flux is independent of the charge distribution inside the surface.View Solution