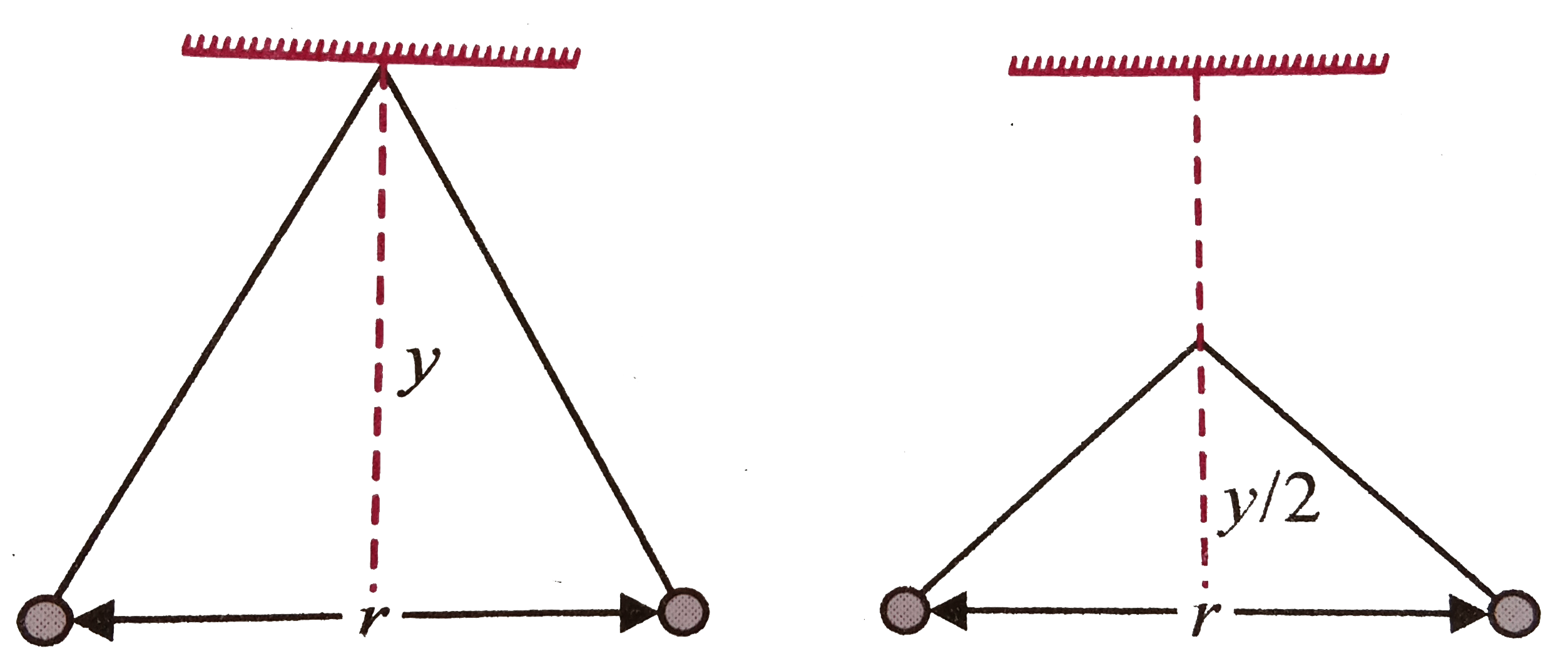
Two pith balls carrying equal charges are suspended from a common point by strings of equal length. The equilibrium separation between them is r. Now the strings are rigidly clamped at half the height . The equilibrium separation between the balls now become .

(r3√2)
(2r√3)
(2r3)
(r√2)2
The correct Answer is:A
from figure , tanθ=Femg⇒r/2y=kq2r2mg
[∴F=kq2r2 from coulomb.s law]
⇒r3∝y⇒r.3∝Y2⇒r.r=121/3⇒r.=r3√2

Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - DISHA PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Exercise - 2 : Concept applicator
24 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - DISHA PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Exercise - 2 : Concept applicator
24 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - DISHA PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - EXERCISE -2 : CONCEPT ALLPLICATOR
30 Videos
- ELECTROMAGNETIC INDUCTION BOOK - DISHA PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - EXERCISE - 2 : Concept Applicator
29 Videos
Similar Questions
Two path balls carrying equal charges are suspended from a common point by strings of equal length, the strings are rightly clamped at half the height. The equilibrium separation between the balls, now becomes :
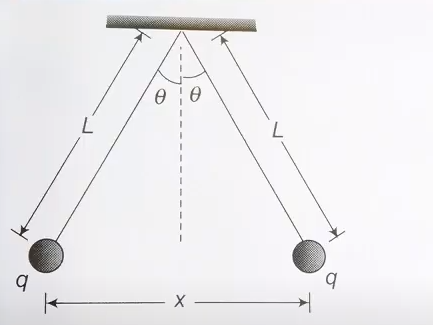
View SolutionTwo point charges are suspended from a given point as shown in figure. Find the equilibrium seperation between them
View Solution
Knowledge Check
Two path balls carrying eqaul chareges are suspended froom a common point by strings of equal length, the strings are rightly clamped at half the height. The equilibrium separation between the balls, now becomes :
 A(2r3)B(1√2)2C(r3√2)D(2r√3)
A(2r3)B(1√2)2C(r3√2)D(2r√3)Two identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'. What is the equilibrium separation when each thread makes a small angle 'θ' with the vertical ?
Ax=(q2l2πε0mg)1/2Bx=(q2l2πε0mg)1/3Cx=(q2l22πε0m2g)1/3Dx=(q2l22πε0m2g2)1/3
Two indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionTwo identical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionTwo indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionTwo identical pith balls are charged by rubbing against each other. They are suspended from a horizontal rod through two strings of length 20 cm each, the separation between the suspension points being 5 cm. in equilibrium, the separation between the balls in 3 cm. Find the mass of each ball and the tension in the strings. the charge on each ball of a magnitude 2.0×10−8C.
View SolutionTwo identical pith balls are charged by rubbing against each other. They are suspended from a horizontal rod through two strings of length 20 cm each, the separation between the suspension points being 5 cm. in equilibrium, the separation between the balls in 3 cm. Find the mass of each ball and the tension in the strings. the charge on each ball a magnitude 2.0×10−8C.
View SolutionTwo identical ball having mass density ρ , mass m and charge q are suspended from a common point by two insulating massless strings of equal length. At equilibrium each string makes an angle theta with the vertical. Now both the balls are immersed in a fluid. At equilibrium, theta remains same. If the mass density of liquid is σ then dielectric constant of liquid will be
View Solution
