A particle of charge −q and mass m moves in a circular orbits of radius r about a fixed charge +Q.The relation between the radius of the orbit r and the time period T is
r=Qq16π2∈0mT2
r3=Qq16π3∈0mT2
r2=Qq16π3∈0MT3
r2=Qq4π3∈0MT3
The correct Answer is:B
By Newton.s second law,
14π∈0Qqr2=mv2r,orv=√Qq4π∈0mr
Now time period, T=2πrv=2πr√Qq4π∈0mr
or r3=(Qq16π3∈0m)T2
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Exercise - 1 Concept builder (Topicwise)58videos
ELECTRIC CHARGES AND FIELDS
- BOOK - DISHA PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - EXERCISE -2 : CONCEPT ALLPLICATOR30videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - DISHA PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - EXERCISE - 2 : Concept Applicator29videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle of charge 'q' and mass 'm' move in a circular orbit of radius 'r' with frequency 'v' the ratio of the magnetic moment to angular momentum is:
A2qvmBqv2mCq2mrDq2m - Question 2 - Select One
A particle of charge q and mass m moves in a circular orbit of radius r with angular speed ω. The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
Aω and qBω,q and mCq and mDω and m - Question 3 - Select One
A particle of charge q and mass m moves in a circular orbit of radius r with angular speed ω. The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
Aω:qBq:mCq:2mDω:m
A particle of charge q and mass m moves in a circular orbit or radius r with angular speed ω. The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
View SolutionA positive charge Q is fixed at a point in space. There is another charge -q, which moves in a circular path of radius r around the given fixed charge . Assume that the electrostatic force between them is the only force acting on them. Calculate time period of revolution of charge .
View SolutionA particle of the charged q and massm moves in a circular orbit of radius r with angular speed ω . The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
View SolutionA particle of charge −q and mass m moves in a circle of radius r around an infinitely long line charge of linear charge density +λ. Then, time period will be
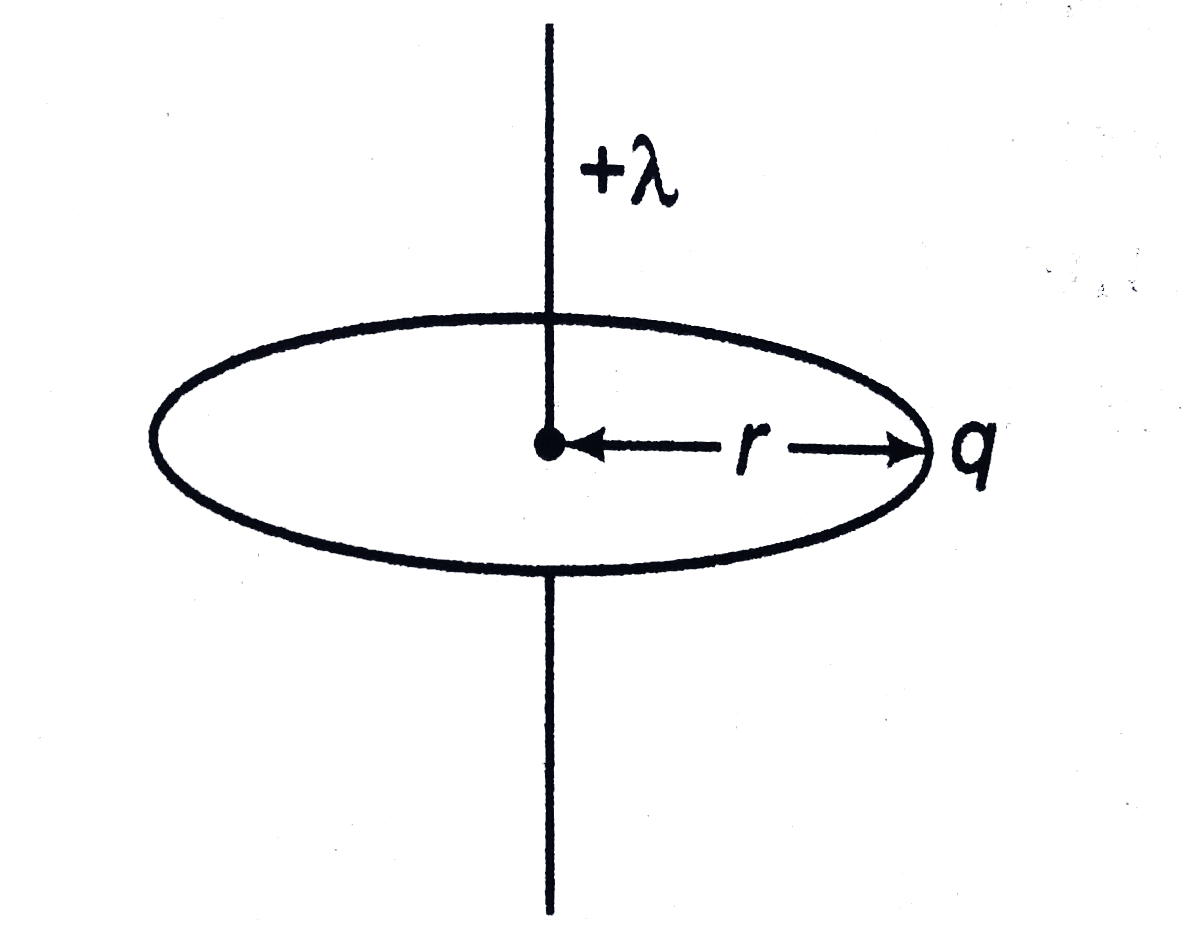 where , k=14πε0)View Solution
where , k=14πε0)View SolutionWhen a charged particle of charge a revolves in a circular orbit of radius r with frequency n, then orbital current will be
View Solution

