Figure shows a uniformaly charged hemisphere of radius R . It has a volume charge density ρ . If the electric field at a point 2R , above its centre is E, then what is the electric field at the point 2R below its centre ?

ρR/6ε0+E
ρR/12ε0−E
−ρR/6ε0+E
ρR/12ε0+E
The correct Answer is:B
Let us complete the sphere. Electric field due to lower part at A is equal to electric field due to upper part at B = E (given) Electric field due to lower part at B = electric field due to full sphere - electric field due to upper part
=kQ(2R)2−E
=14πε0ρ(4/3)πR34R2−E=ρR12ε0−E

Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - DISHA PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Exercise - 1 Concept builder (Topicwise)
58 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - DISHA PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - EXERCISE -2 : CONCEPT ALLPLICATOR
30 Videos
- ELECTROMAGNETIC INDUCTION BOOK - DISHA PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - EXERCISE - 2 : Concept Applicator
29 Videos
Similar Questions
Figure shows a uniformly charged hemisphere of radius R. It has a volume charge density ρ. If the electric field at a point 2R, above the its center is E, then what is the electric field at the point 2R below its center?

View SolutionA ring of radius R is placed in the plane its centre at origin and its axis along the x-asis and having uniformly distributed positive charge. A ring of radius r(<<R) and coaxial with the larger ring is moving along the axis with constant velcity , then the variation of electrical flux (ϕ) passing through the smaller ring with position will be best represent by :
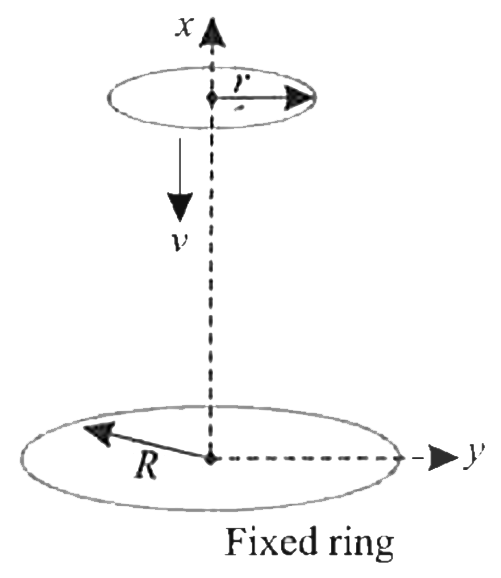
View Solution
Knowledge Check
Figure shows a uniformly charged hemisphere of radius R. It has a volume charge density ρ. If the electric field at a point 2R, above the its center is E, then what is the electric field at the point 2R below its center?
 AρR/6ε0+EBρR/12ε0−EC−ρR/6ε0+EDρR/12ε0+E
AρR/6ε0+EBρR/12ε0−EC−ρR/6ε0+EDρR/12ε0+EA sphere of radius R has a charge density σ. The electric intensity at a point at a distance r from its centre is
AE=σR2∈0kr2BE=σ∈0kCE=R2DE=∈0kr2σ2An insulated sphere of radius r haas a uniform volume charge density λ. The electric field at a point A, which is at distance r from its centre is given by (R>r)
AZeroBRλ/3∈0C2rλ3∈0Drλ3∈0
There is a hemisphere of radius R having a uniform volume charge density ρ. Find the electric potential and field at the centre
View Solution(a) Use Gauss's law to show that due to a uniformly charged spherical shell of radius R, the electric field at any point situated outside the shell at a distance r from its centre is equal to the electric field at the same point, when the entire charge on the shell were concentrated at its centre. Also plot the graph showing the variation of electric field with r, for r≤R and r≥R. (b) Two point charges of +1μC and +4μC are kept 30 cm apart. How far from the +1μC charge on the line joining the two charges, will the net electric field be zero ?
View SolutionUse Gauss's law to show that due to uniformly charged spherical shell of radius R, the electric field at any point situated outside the shell at a distance r from its centre is equal to the electric field at the same point, when the entire charge on the shell were concentrated at its centre. Also plot the graph showing the variation of electric field with r, for r≤R and r≥R.
View SolutionA shere of radius a is uniformaly charged thoughout its volume with a volume change density of σ. Calculate the electeric field at a distance r form the centre of the sphere when(i)r<a(ii)whenr>a.
View SolutionAn insulated sphere of radius R has a uniform volume charge density λ. The electric field at a point A, which is at distance r from its center is given by (R>r)
View Solution
