A battery is connected to a series RL circuit at time t = 0. At what multiple of τL will the current be 1.00% less than its equilibrium value?
To solve the problem, we need to determine the time t at which the current I in an RL circuit is 1% less than its maximum (equilibrium) value Imax.
1. Understand the Current Equation:
The current I(t) in an RL circuit as a function of time is given by:
I(t)=Imax(1−e−tτL)
where τL is the time constant of the RL circuit.
2. Set Up the Equation for 1% Less Current:
We need to find the time t when the current I(t) is 1% less than Imax. This means:
I(t)=Imax−0.01Imax=0.99Imax
3. Substitute into the Current Equation:
Substitute I(t) into the equation:
0.99Imax=Imax(1−e−tτL)
4. Divide Both Sides by Imax:
Since Imax is not zero, we can divide both sides by Imax:
0.99=1−e−tτL
5. Rearrange the Equation:
Rearranging gives:
e−tτL=1−0.99=0.01
6. Take the Natural Logarithm:
Taking the natural logarithm of both sides:
−tτL=ln(0.01)
7. Solve for t:
Rearranging gives:
t=−τLln(0.01)
8. Calculate ln(0.01):
We know that:
ln(0.01)=ln(1100)=−ln(100)=−2ln(10)≈−2×2.303≈−4.605
Therefore:
t=−τL×(−4.605)=4.605τL
Final Answer:
The time t at which the current is 1% less than its equilibrium value is:
t=4.605τL
The current I(t) in an RL circuit as a function of time is given by:
I(t)=Imax(1−e−tτL)
where τL is the time constant of the RL circuit.
We need to find the time t when the current I(t) is 1% less than Imax. This means:
I(t)=Imax−0.01Imax=0.99Imax
Substitute I(t) into the equation:
0.99Imax=Imax(1−e−tτL)
Since Imax is not zero, we can divide both sides by Imax:
0.99=1−e−tτL
Rearranging gives:
e−tτL=1−0.99=0.01
Taking the natural logarithm of both sides:
−tτL=ln(0.01)
Rearranging gives:
t=−τLln(0.01)
We know that:
ln(0.01)=ln(1100)=−ln(100)=−2ln(10)≈−2×2.303≈−4.605
Therefore:
t=−τL×(−4.605)=4.605τL
The time t at which the current is 1% less than its equilibrium value is:
t=4.605τL
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
45 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
13 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHECKPOINTS
9 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
- ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT EXERCISE - Practice Questions (Integer)
7 Videos
Similar Questions
At t = 0, a battery is connected to a series arrangement of a resistor and an inductor. At what multiple of the inductive time constant will the energy stored in the inductor's magnetic field be 0.500 of its steady-state value?
View SolutionRL circuit, current during the transition
A solenoid has an inductance of 53 mH and a resistance of 0.37 Ω . If the solenoid is connected to a battery, how long will the current take to reach half its final equilibrium value? (This is a real solenoid because we are considering its small, but nonzero, internal resistance.)
View Solution
Knowledge Check
An ideal inductor, (having initial current zero) a resistor and an ideal battery are connected in series at time t=0. At any time t, the battery supplies energy at the rate PB, the resistor dissipates energy at the rate PR and the inductor stores enegy at the rate PL.
APB=PR+PL for all times t.BPR<PL for all times tCPR<PL only near the starting of the circuit.DPR>PL only near the starting of the circuit.A circuit consists of a coil, a switch and a battery, all in series. The interval resistance of the battery is negligible compared with that of the coil. The switch is originally open. It is thrown closed, after a time interval Δt. The current in the circuit reaches 80.0% of its final value. The switch then remains closed for a time interval much longer than Δt. The wires connected to the terminals of the battery are then short circuited with another wire and removed from the battery, so that the current is uninterrupted.
At an instant that is a time interval Δt. After the short circuit, the current is what percentage of its maximum value?A20.0%B8.0%C4.0%D10.0%When a battery is connected across a series combination of self-inductance L and resistance R, the variation in the current I with time t is the best represented by
A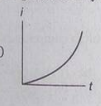 B
B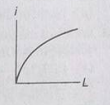 C
C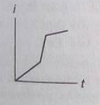 D
D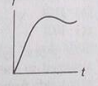
An inductor of 0.2 H is connected to a 5 V battery. The current flowing through the inductor is 10 A. The inductor is now removed from the battery and is connected in series to a capacitor to a 5 V AC source. Calculate the rms value of current if current and voltage in circuit is in phase.
View SolutionA coil having an inductance L and a resistance R is connected to a battery of emfε. Find the time elapsed before (a) the current reaches half its maximum value, (b) the power dissipated in heat reaches half its maximum value and © the magnetic field energy stored in the circuit reaches half its maximum value.
View SolutionA circuit consisting of a capacitor with capacitance C and a resistance R connected in series was connected at the moment t=0 to a source of ac voltage V=Vmcosωt . Find the current in the circuit as a function of time t.
View SolutionWhen a battery is connected across a series combination of self-inductance L and resistance R, the variation in the current I with time t is the best represented by
View SolutionWhen a battery is connected across a series combination of self inductance L and resistance R , the variation in the current i with time t is best represented by
View Solution
