A coherent parallel beam of microwaves of wavelength λ=0.5mm falls on aYoung's double- slit apparatus. The separation between the slits is 1.0 mm. The intensity of microwaves is measured on a screen placed parallel to the plane of the slits at a distance of 1.0 m from it as shown in Fig. 2.42.
If the incident beam makes an angle or 30∘ with the x-axis (as in the dotted arrow shown in the figure), find the y-coordinates of the first minima on either side of the central maximum.
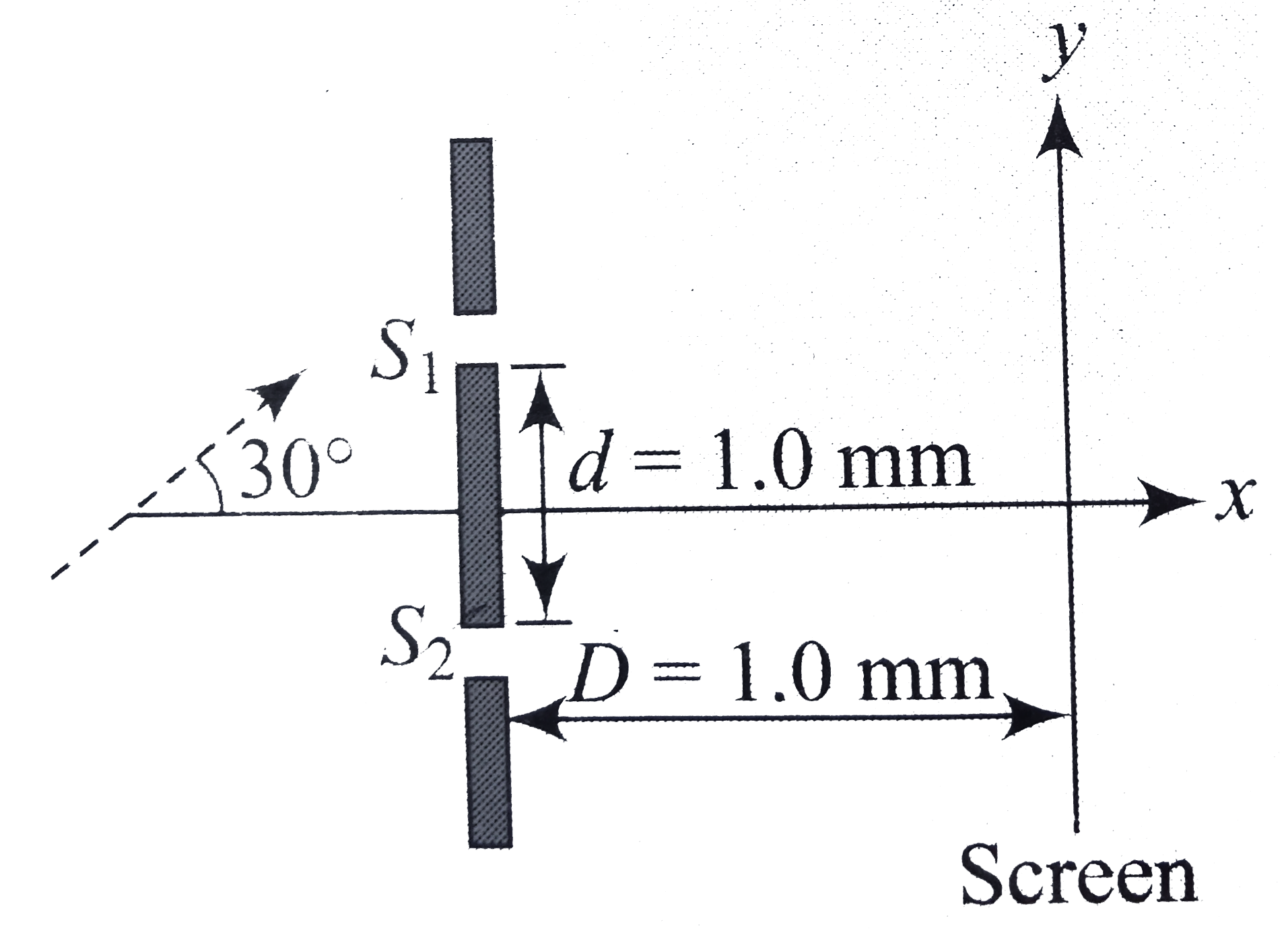
When the incident beam falls nor- mally on the slits S1 and S2, the path difference at the central point P0 of the screen is zero. Hence, we have the central maximum at P0. At the minima, the path difference between the waves is Δ=[m+(1/2)]λ.

This is a classic case when the wavelength of the light is comparable to the slit separation d. So we cannot apply the equation for fringe width as in Eq. 35-19.
Calculation: Let the minima appear along directions θ with respect to the incident direction. Coherent waves from S1 and S2 along this direction are brought to a focus at P. It is clear that the path difference between the waves from S1 and S2 on reaching P is
Δ=dsinθ.
The interference minima will appear on the screen if
Δ=(m+12)λ
dsinθ=(m+12)λ
where m is an integer. Thus, the direction of minima is given by
sinθ=(m+12)×λd
It is given that d = 1.0 mm and λ=0.5mm. Therefore,
sinθ=(m+12)×(0.51.0)=12(m+12) (35−22)
The allowed values of m are those integers for which sinθ is not more than +1 or less than -1. These values are m=1, 0, -1, and -2. Hence, four minima will be observed. If follows from the figure that
tanθ=yD⇒y=Dtanθ
y=Dsinθ(1−sin2θ)1/2 (35−23)
The first minima above the central maximum (P0) corresponds to m = 0. Using Eq. 36-17, we have sinθ=1/4 for this minimum. Using this value in Eq. 35-22 the distance of the first minimum P1 from P9 is
y1=(1.0m)×(1/4)[1−(1/16)]1/2=1√15m.
This is the y coordinate of the first minimum P1 above P0.
The second minima above P0 corresponds to m = 1, for which, we have from Eq. 36-17, sinθ=3/4. Using this value in Eq. 35-24, the y coordinate of the second minimum P2 above P1 is
y2=(1.0m)×(3/4)[1−(9/16)]1/2=3√7m
The first minimum P1.below P0 corresponds to m = -1, for which sinθ=−1/4. The y coordinate of this minimum P1. is
y1.=−1√15m.
The second minimum below P2. corresponds to m= -2 for which sinθ=−3/4. The y coordinate of P2. is
P2.=−3√7m. (Answer)
Related Playlists
- BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - CHECKPOINT6videos
INTERFERENCE AND DIFFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PROBLEMS61videos
INTERFERENCE AND DIFFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS(Integer Type)6videos
HYDROGEN ATOM
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)4videos
MAGNETIC FIELDS DUE TO CURRENTS
Knowledge Check
- Question 1 - Select One
A coherent parallel beam of microwaves of wavelength λ=0.5mm falls on aYoung's double- slit apparatus. The separation between the slits is 1.0 mm. The intensity of microwaves is measured on a screen placed parallel to the plane of the slits at a distance of 1.0 m from it as shown in figure
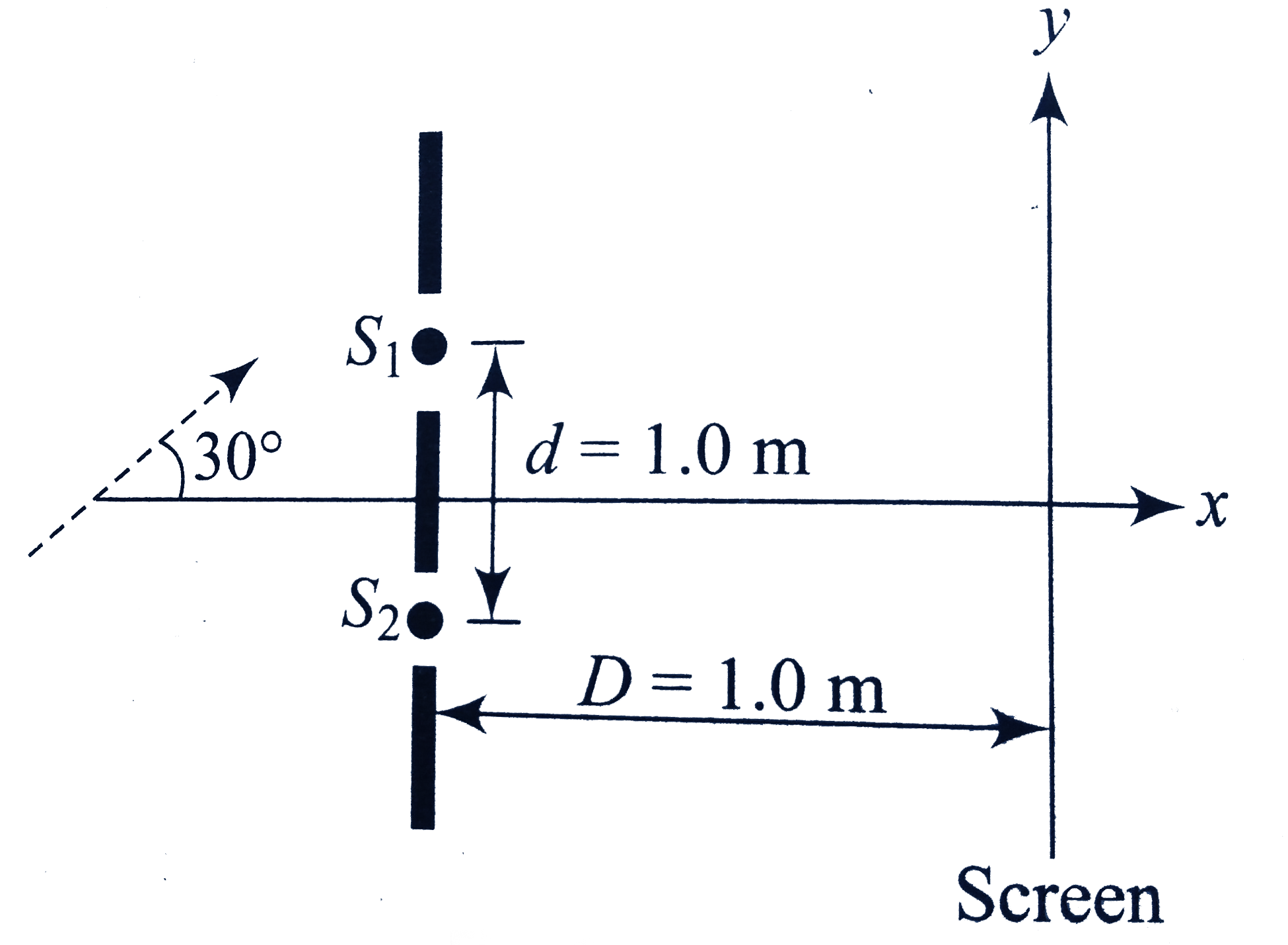
If the incient beam falls normally on the double-slit apparatus, find the order of the interference minima on the screenAOnly the first order minima are possibleBOnly the first order and second minima are possibleCTotal six minima appear on the screenDTotal eight minima appear on the screen - Question 1 - Select One
In Young's double slit experiment, white light is used. The seperation between the slits is kept 1mm and intensity is observed on screen distance 2m from the plane of the slits. At a point on the screen directly opposite to the either slit which of the following wavelength is not present
AultravioletBredCYellowDviolet - Question 1 - Select One
Light of wavelength λ=5890Å fall on a double-slit arrangement having separation d=0.2mm. A thin lens of focal length f=1m is placed near the slits. The linear separation of fringes on a screen placed in the focal plane of the lens is
A3 mmB4 mmC2 mmD1 mm - Question 1 - Select One
In Young's double slit experiment, the distance between the two slits is 0.1mm and the wavelength of light used is 4×10−7m. If the width of the fringe on the screen is 4 mm , the distance between screen and slit is
A0.1mmB1 cmC0.1cmD1 m - Question 1 - Select One
White light of wavelength in range 400 nm to 700 nm is incident normaly on a young's double slit experiment apparatus. The distance betweenn slits is d=1 mm and distance between plane of the slits and screen in 0.8 m. At a point on the screen just in front of one of the slits the missing wavelength is (are)
A533.3 nmB416.7 nmC666.7 nmD577.7 nm - Question 1 - Select One
A parallel beam of light of wavelength 600 nm is incident normally on a slit of width d. If the distance between the slits and the screen is 0.8 m and the distance of 2nd order maximum from the centre of the screen is 15 mm. The width of the slit is
A40μmB80μmC160μmD200μm - Question 1 - Select One
The Young's double slit experiment the wavelength of light λ=4×10−7m and separation between the slits is d=0.1mm. If the frintge width is 4mm then the seperation between the slits and the screen will be
A100 mmB1mC106mD10Å
Similar Questions
A coherent parallel beam of microwaves of wavelength A = 0.5 mm fails on a Young's double slit apparatus. The separation between maxima is measured on a screen placed paraiiei to the plane, of the slits at a distance of 1.0 m from it as shown in figtird. The separation between the slits is 2d - 1mm.
(a) If the incident beam fails normally on the double slit apparatus, find the y-coordinates of all the interface minima of the screen.
(b) If the incident beam makes an angle of 30° with the x-axis (as shown in fig. find the y-coordinates of the first minima on either side of the central maximum.
 View Solution
View SolutionA parallel beam of monochromatic light is used in a Young's double slit experiment. The slits are separated by a distance d and the screen is placed parallel to the plane of the slits. Show that if the incident beam makes an angle θ=sin−1(λ2d) with the normal to the plane of the slits, there will be a dark fringe at the centre Po of the pattern.
View SolutionA parallel beam of monochromatic light of wacelength λ used in a Young's double slit experiment. The siits are separated by a distance d and the screen is placed parallel to the plane of the slits. The incident beam makes an angle θ=sin−1(λ2d) with the normal to the slits. A transparent sheet of refractive index 'μ' and thickness t=λ2(μ−1) is introduced infront of one of the slit. find the intensity at the geometrical centre.
View Solution

