Light from source S is incident on the Fresnel biprism shown in Figure. The light beams refracted by the different faces of the prism partly overlap and produce an interference pattern on a screen on its section AB.
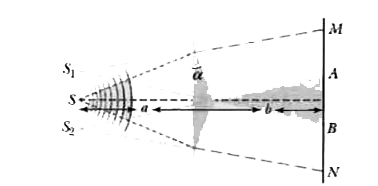
Find the distance between adjacent interference fringes if the distance from the source to the prism is a = 1 m and that from the prism to the screen is b = 4 m. The angle of refraction of the prism is a=2×10−3 rad.
The glass of prism has a refractive index of n = 1.5. The wavelength of the light is λ=6000Å.
KEY IDEA
To find the distance d it is first necessary to calculate the distance l between the virtual source S1 and S2 located at the point of intersection to the continuation of the rays refracted by the prism faces. For this purpose, it will be the simplest to consider the path of the ray normally incident on the face of the prism.
Calculation: No such ray actually exists, but it can be plotted by mentally extending the upper prism downward.
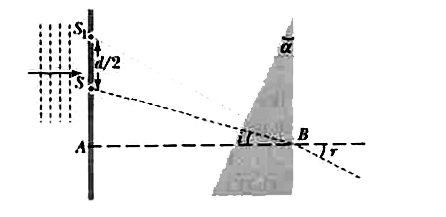
All the beams from point source refracted by a prism can be assumed to converge at a point. Since the refracting angle of the prism is small (the prism is thin), the virtual images S1 and S2 of the source can be regarded as lying at the same distance from the prism as source S. It can be seen from figure that i=α and SA=aα. According to the law of refraction, r≅nα. Considering the triangle AS1B, we can write
d2+aα≅aαn
Hence,
d=2aα(n−1).
We find that
β=λDd=λ(a+b)2aα(n−1)=0.15cm.
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - CHECKPOINT
6 Videos
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PROBLEMS
61 Videos
- HYDROGEN ATOMBOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS(Integer Type)
6 Videos
- MAGNETIC FIELDS DUE TO CURRENTSBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)
4 Videos
Similar Questions
Two coherent sources of light interfere and produce fringe pattern on a screen . For central maximum phase difference between two waves will be
View SolutionA fresnel biprism is used to form the inerference fringes. The distance between the source and the biprisim is 20 cm and that between the biprism and the screen is 80 cm. If A= 6563 A and the separation between the virtual sources is 3.6 mm, then the fringes width (in mm) is.
View Solution
Knowledge Check
In a biprism experiment the distance of source from biprism is 1 m and the distance of screen from biprism is 4 meters. The angle of refraction of biprism is 2×10−3 radians. μ of biprism is 1.5 and the wavelength of light used is 6000 Å. How many fringes will be seen on the screen ?
A4B5C3D6Two coherent sources of light interfere and produce fringe pattern on a screen . For central maximum phase difference between two waves will be
AzeroBπC3π2Dπ2Two coherent sources of light interfere and produce fringe pattern on a screen . For central maximum phase difference between two waves will be
AπB3π/2Cπ/2DZero
Monochromatic light from a narrow slit illuminates two parallel slits producing an interference pattern on a screen. The separation between the two slits is now doubled and the distance between the screen and the slits is reduced to half. The fringe width
View SolutionIf S1andS2 are two point sources emitting light in phase , then what is the shape of interference fringes formed on the screen ?
View SolutionMonochromatic light from a narrow slit illuminates two parallel slits producing an interference pattern on a screen. The separation between the two slits is now doubled and the distance between the screen and the slits is reduced to half. The fringe width
View SolutionTwo sources give interference pattern which is observed on a screen, D distance apart from the sources. The fringe width is 2 w . If the distance D is now doubled, the fringe width will
View Solution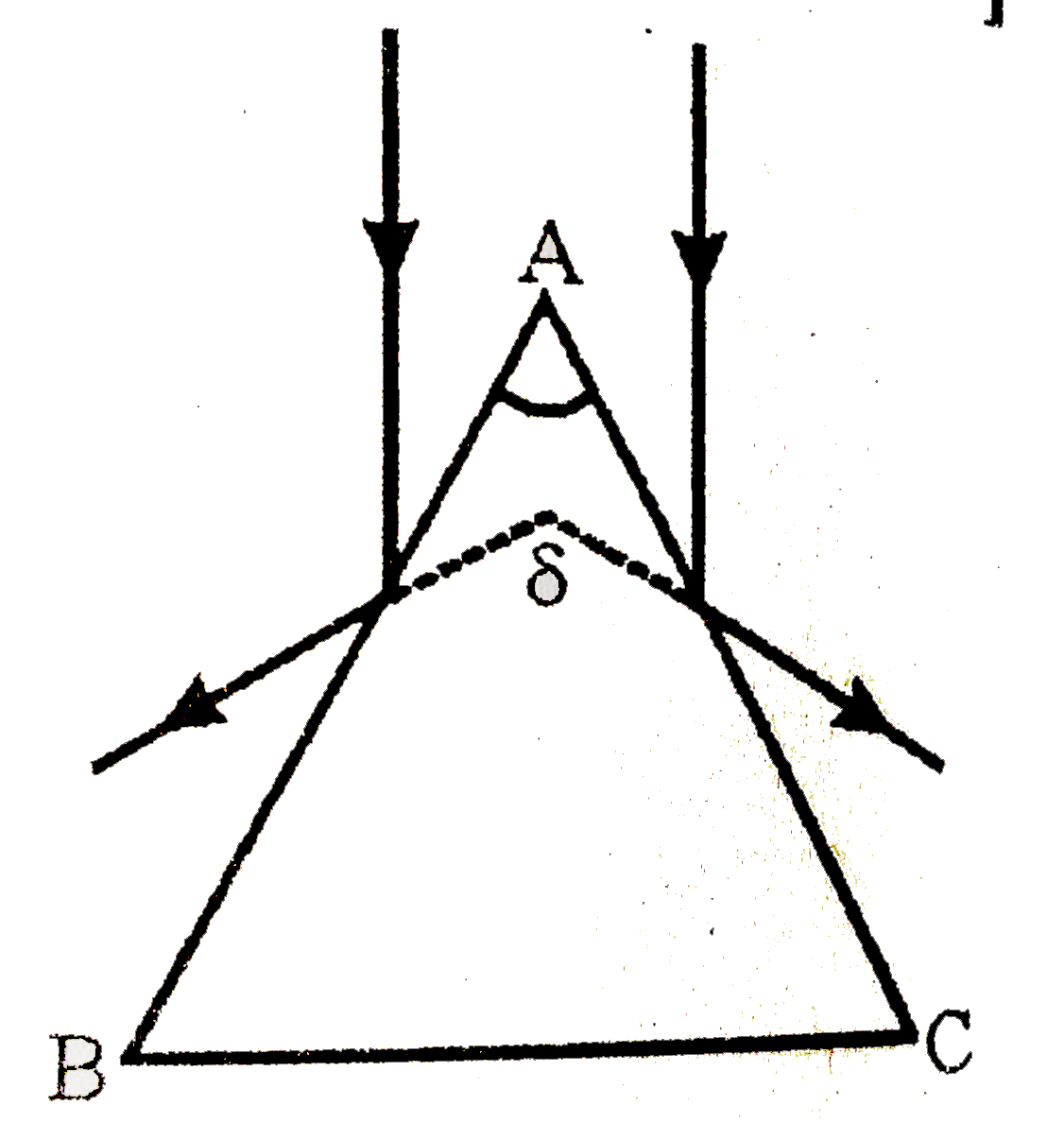
A parallel beam of light is incident on a prism as shown in figure. Such that the rays get reflected from opposite faces. The angle of deviation δ between reflected rays from faces AB and AC is-
View Solution
