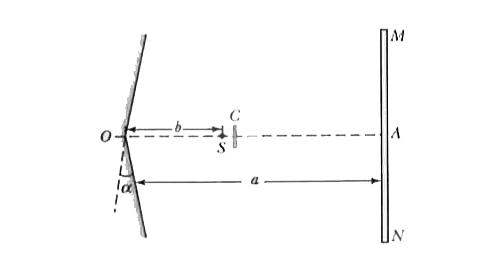
Two flat mirrors form an angle close to . A source of light S is placed at an equal distance b from the mirrors. Find the distance between adjacent interference fringes on screen MN at a distance , from the point of intersection of the mirrors. The wavelength of the light is equal to . Shield C does not allow the light to pass directly from the source to the screen.
KEY IDEA
As you might recall, the object and image distances from the mirror are equal. This would imply that the image is located behind the mirror at an angle behind the line OA. Similarly, for the second mirror. The image should also be located at a distance b from the point of intersection of the mirrors. This can be seen in Figure.
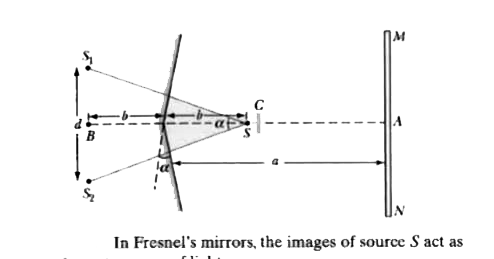
This is again a situation where the two mirrors are producing the two images. These two images act as coherent sources.
Calculation: The distance between interference bands is . In our case , and is the distance between the images and of the source in the flat mirrors. The value of d can be found from triangle :
Hence,
.
Learn: The light from source S, after reflection from and , splits into two beams which illuminate different regions of the screen. The formation of interference fringes can be interpreted as due to two wave- fronts coming from virtual sources and which are images of S in mirrors and , respectively. The lin- ear distance between and is, therefore, equivalent to separation d between the slits.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - CHECKPOINT6videos
INTERFERENCE AND DIFFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PROBLEMS61videos
INTERFERENCE AND DIFFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS(Integer Type)6videos
HYDROGEN ATOM
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)4videos
MAGNETIC FIELDS DUE TO CURRENTS
Similar Questions
The figure shows a monochromatic ray of light traveling across parallel interfaces, from an original material a, through layers of materials b and c, and then back into material a. Rank the materials according to the speed of light in them, greatest first.
 06:46View Solution
06:46View Solution
In Figure, a broad bcam Incident light of light of wavelength 630 nn is sent directly downward through the top plate of a pair of glass plates touching at the left end. The air between the plates acts as a thin film, and an interference pattern can be seen from above the plates. Initially, a dark fringe lies at the left end, a bright fringe lies at the right end, and nine dark fringes lie between those two end fringes. The plates are then very gradually squeezed together at a constant rate to decrease the angle between them. As a result, the fringe at the right side changes between being bright to being dark every 15.0 s. (a) At what rate is the spacing between the plates at the right end being changed? (b) By how inuch has the spacing there changed when both left and right ends have a dark fringe and there are five dark fringes between them?05:51View SolutionThe radius of hydrogen atom in its ground state is 5.3×10−11m. After collision with an electron, it is found to have a radius of 21.2×10−11m. What is the principal quantum number of the final state of the atom?
04:53View SolutionA steady current I goes through a wire loop PQR having shape of a right angle triangle with PQ=3x,PR=4xandQR=5x. If the magnitude of the magnetic field at P due to this loop is k(μ0I48πx), find the value of K.
08:45View SolutionIn Lloyd's mirror experiment (Fig.) a light wave emitted directly be the source S (narrow slit) interferes with the wave reflected form a mirror M. As s result, an interference fringe pattern is

formed on the screen Sc. the source and the mirror are separated by a distance l=100cm.At a certain position of the source the fringe width on the screen was equal to Δx=0.25mm, and after source was moved away from the mirror plane by Δh=0.60mm, the fringe width decreased η=1.5 times. Find the wavelength of light.04:36View SolutionTwo mirror M1 and M2 make an angle ϕ with line AB. A point source S is kept at a distance r from the point of intersection of mirror. A small hemispherical annular mask is kept close to S so that no ray emanting from S directly reaches the screen kept at a distance b from the source. Interference pattern of rays reflected from M1 and M2 is oberved on the screen. Find the fringe width of this interference pattern λ= wavelength of light being emitted by source.
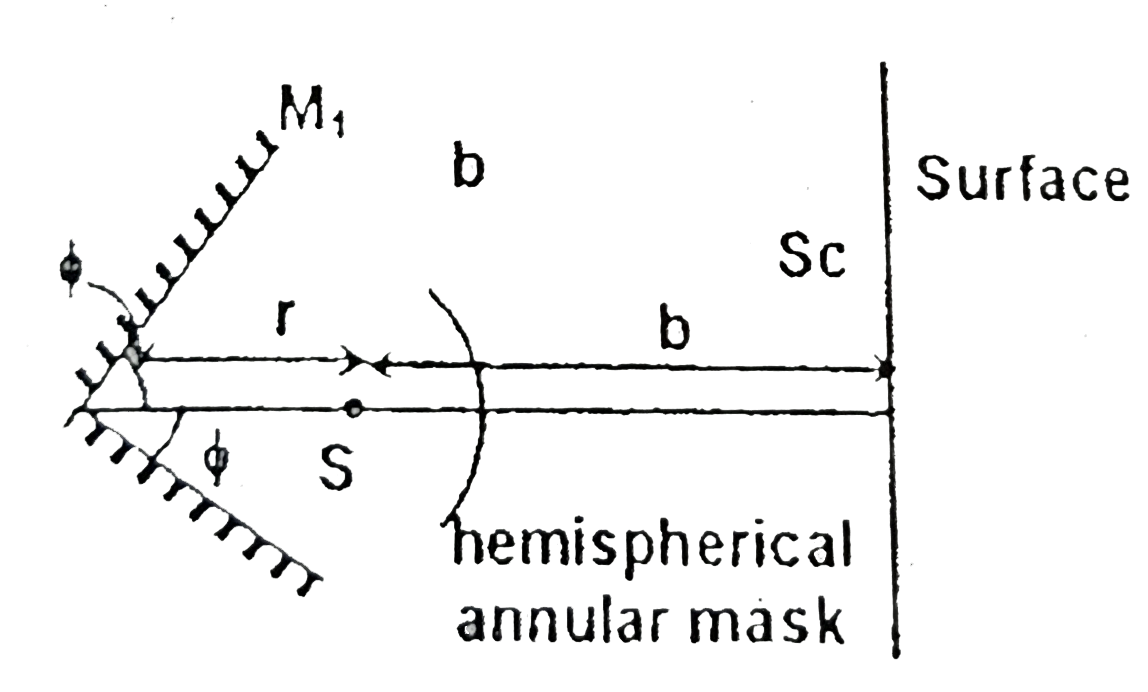 View Solution
View SolutionIn Lloyd's single mirror interference experiment, the source slit is at a distance of 2 mm from the plane mirror . The screen is kept at a distance of 1.5m from the source . If light of wavelength 5890 Å is used, calculate the fringe width.
03:43View SolutionLight source of wavelength 400 nm used in a Lloyd's mirror, lies 1 mm above the plane mirror. Find the distance of first minima above the mirror. Distance of the screen from the plane of the sources is 2 m.
09:42View SolutionTwo plane mirrors makes an angle of 120^(@) with each other. The distance between the two images of a point source formed in them is 20 cm . Determine the distance from the light source of the point where the mirrors touch, the light source lies on the bisector of the angle formed by the mirrors.
View SolutionIn a Lloyds's mirror experiment as narraow slit S iransmitting a light of wavelength λ is placed 3 mm above a small plane mirror ( as shown). The light coming directly from the the slit and that coming after the reflection interfere on a screen placed at a distance of 90 cm from the slit. Length of mirror is 2 mm and the middle point of mirror is 2 mm from point P.
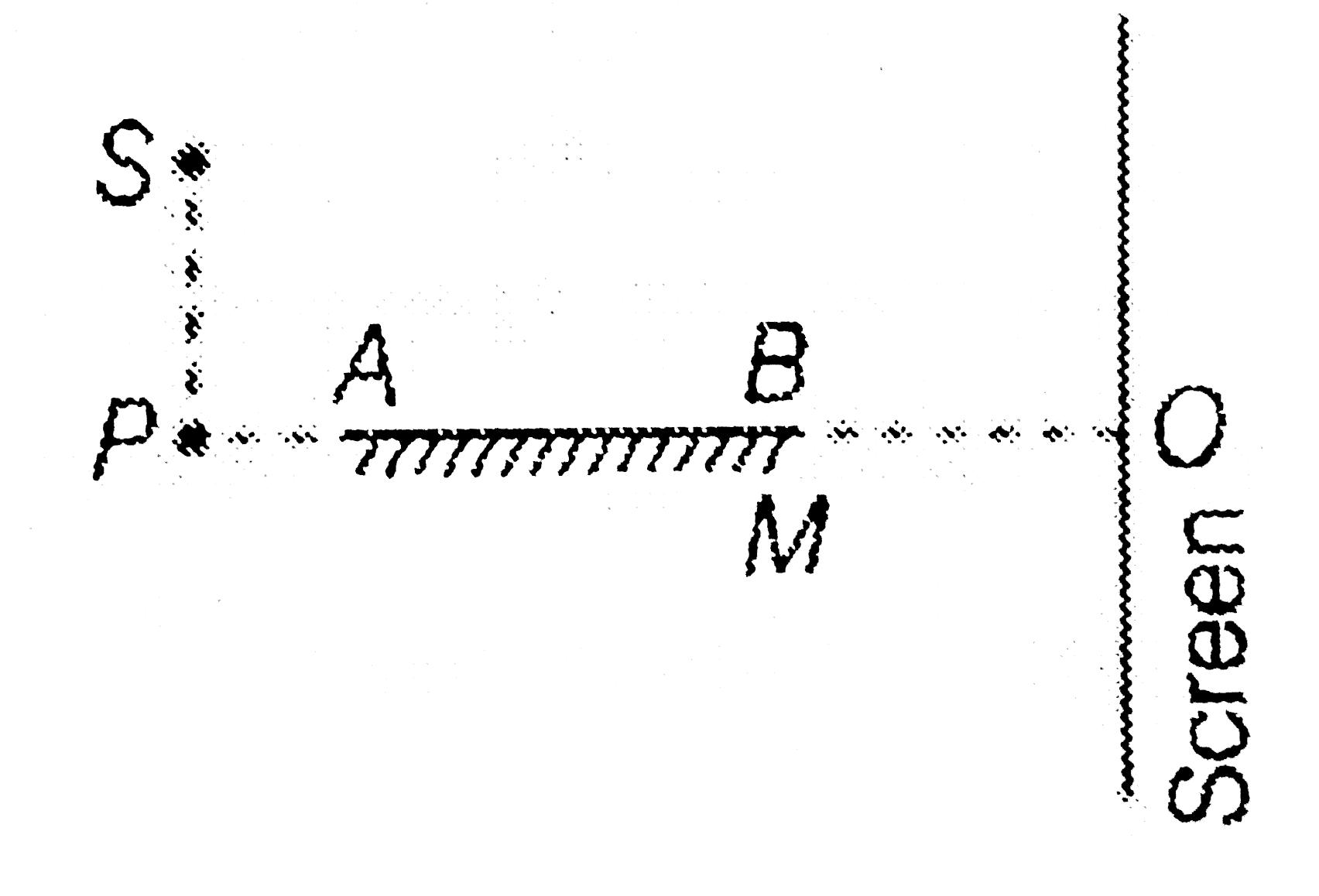
If the mirror is shifted towards left then how does the fringe pattern on screen changes ?07:30View SolutionThe distance between two coherent sources is 1 mm. The screen is placed at a distance of 1 m from the sources. If the distance of the third bright fringe is 1.2 mm from the central fringe, the wavelength of light used is
02:09View Solutionप्रकाश का एक बिंदु स्रोत S, दीवार पर ऊर्ध्वाधर लटके d चौड़ाई वाले समतल दर्पण S के केंद्र से L दूरी पर स्थित है | दर्पण से 2L दूरी पर उसके समान्तर रेखा के अनुदिश एक व्यक्ति दर्पण के सामने से चित्रानुसार गुजरता है | वह अधिकतम दूरी जहाँ वह व्यक्ति बिंदु स्रोत का प्रतिबिम्ब दर्पण में देख सकता है |
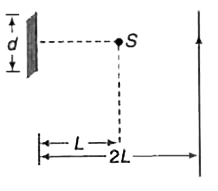 01:40View Solution
01:40View SolutionA point source of light S, placed at a distance L in front of the centre of a mirror of width d, hangs vertically on a wall. A man walks in front of the mirror along a line parallel to the mirror at a distance 2L from it as shown in figure. Find the greatest distance over which he can see the image of the light source in the mirror.
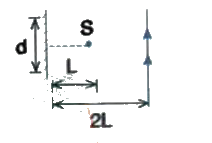 01:32View Solution
01:32View Solutionएक एकल दर्पण के कारण व्यतिकरण पर प्रयोग में, स्त्रोत S(संकड़ी स्लिट) द्वारा सीधे उत्सर्जित एक प्रकाश तरंग 2mm लम्बाई के दर्पण Mसे परावर्तित तरंग के साथ व्यतिकरण करती है। स्रोत व पर्दे के बीच पृथकता दूरी 90 cm होती है। स्रोत S बिन्दु P से 3mm की ऊँचाई पर है तथा दर्पण का मध्य बिन्दु, बिन्दु P से 2mm की दूरी पर है। बिन्दु Pा दर्पण समान तल में हैं तथा पर्दे का तल इस तल के लम्बवत् है।

यदि फिन्ज चौडाई 0.1 mm है तो प्रयुक्त प्रकाश की तरंगदैर्ध्य क्या होती है?03:26View SolutionYou are standing at a distance 2 metre from a plane mirror.
What is the distance of your image from the mirror ?03:19View SolutionIn a Lloyds's mirror experiment as narrow slit S transmitting a light of wavelength λ is placed 3 mm above a small plane mirror ( as shown). The light coming directly from the the slit and that coming after the reflection interfere on a screen placed at a distance of 90 cm from the slit. Length of mirror is 2 mm and the middle point of mirror is 2 mm from point P.

If the mirror is shifted towards left then how does the fringe pattern on screen changes ?01:50View Solution

