A transparent plastic block with a thin wedge of air at the right. (The wedge thickness is exaggerated in the figure.) A broad beam of red light, with wavelength λ=632.8nm, is directed downward through the top of the block (at an incidence angle of 0∘). Some of the light that passes into the plastic is reflected back up from the top and bottom surfaces of the wedge, which acts as a thin film (of air) with a thickness that varies uniformly and gradually from LL at the left-hand end to LR at the righthand end. (The plastic layers above and below the wedge of air are too thick to act as thin films.) An observer looking down on the block sees an interference pattern consisting of six dark fringes and five bright red fringes along the wedge. What is the change in thickness ΔL(=LR−LL) along the wedge?

KEY IDEAS
(1) The brightness at any point along the left-right length wedge. of the air wedge is due to the interference of the waves reflected at the top and bottom interfaces of the wedge.
(2) The variation of brightness in the pattern of bright and dark fringes is due to the variation in the thickness of the wedge. In some regions, the thickness puts the reflected waves in phase and thus produces a bright reflection (a bright red fringe). In other regions, the thickness puts the reflected waves out of phase and thus produces no reflection (a dark fringe).
Organizing the reflections: Because the observer sees more dark fringes than bright fringes, we can assume that a dark fringe is produced at both the left and right ends of the wedge. Thus, the interference pattern is that shown in Figure.
We can represent the reflection of light at the top and bottom interfaces of the wedge, at any point along its length, in which L is the wedge thickness at that point. Let us apply this figure to the left end of the wedge, where the reflections give a dark fringe.
We know that, for a dark fringe, the waves of rays r1 and r2 must be out of phase. We also know that the equation relating the film thickness L to the light.s wavelength λ and the film.s index of refraction n2 is either Eq. 35-50 or Eq. 35-51, depending on the reflection phase shifts. To determine which equation gives a dark fringe at the left end of the wedge, we should fill out an organizing table.
At the top interface of the wedge, the incident light is in the plastic, which has a greater n than the air beneath that interface. So, we fill in 0 underr1 in our organizing table. At the bottom interface of the wedge, the incident light is in air, which has a lesser n than the plastic beneath that interface. So we fill in 0.5 wavelength under r2. So, the phase difference due to the reflection shifts is 0.5 wavelength. Thus the reflections alone tend to put the waves of r1 and r2 out of phase.
Reflections at left end: Because we see a dark fringe at the left end of the wedge, which the reflec- tion phase shifts alone would produce, we do not want the path length difference to alter that condition. So, the path length difference 2L at the left end must be given by
2L=integer×λn2
which leads to Eq. 35-49:
2L=mλn2, for m = 0, 1, 2, .... (35−53)
Reflections at right end: Equation 35-53 holds not only for the left end of the wedge but also for any point along the wedge where a dark fringe is observed, including the right end, with a different integer value of m for each fringe. The least value of n is associ- ated with the least thickness of the wedge where a dark fringe is observed. Progressively greater values of m are associated with progressively greater thicknesses of the wedge where a dark fringe is observed. Let mL be the value at the left end. Then the value at the right end must be mL+5 because, the right end is located at the fifth dark fringe from the left end.
Thickness difference: To find ΔL, we first solve Eq. 35-53 twice-once for the thickness LL at the left end and once for the thickness LR at the right end:
LL=(mL)λ2n2,LR=(mL+5)λ2n2. (35−54)
We can now subtract LL from LR and substitute n2=1.00 for the air within the wedge and λ=632.8×10−9m,
ΔL=LR−LL=(mL+5)λ2n2−mLλ2n2=52λn2
=1.58×10−6m. (Answer)
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - CHECKPOINT6videos
INTERFERENCE AND DIFFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PROBLEMS61videos
INTERFERENCE AND DIFFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS(Integer Type)6videos
HYDROGEN ATOM
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)4videos
MAGNETIC FIELDS DUE TO CURRENTS
Similar Questions
The figure shows a monochromatic ray of light traveling across parallel interfaces, from an original material a, through layers of materials b and c, and then back into material a. Rank the materials according to the speed of light in them, greatest first.
 07:09View Solution
07:09View Solution
In Figure, a broad bcam Incident light of light of wavelength 630 nn is sent directly downward through the top plate of a pair of glass plates touching at the left end. The air between the plates acts as a thin film, and an interference pattern can be seen from above the plates. Initially, a dark fringe lies at the left end, a bright fringe lies at the right end, and nine dark fringes lie between those two end fringes. The plates are then very gradually squeezed together at a constant rate to decrease the angle between them. As a result, the fringe at the right side changes between being bright to being dark every 15.0 s. (a) At what rate is the spacing between the plates at the right end being changed? (b) By how inuch has the spacing there changed when both left and right ends have a dark fringe and there are five dark fringes between them?03:37View SolutionThe radius of hydrogen atom in its ground state is 5.3×10−11m. After collision with an electron, it is found to have a radius of 21.2×10−11m. What is the principal quantum number of the final state of the atom?
05:08View SolutionA steady current I goes through a wire loop PQR having shape of a right angle triangle with PQ=3x,PR=4xandQR=5x. If the magnitude of the magnetic field at P due to this loop is k(μ0I48πx), find the value of K.
05:08View SolutionA block of mass m is released from the top of a wedge of mass M as shown in figure. Find the displacement of wedges on the horizontal ground when the block reaches the bottom of the wedges. Neglect friction everywhere.
05:08View SolutionA block of mass m is placed at the bottom of a massless smooth wedge which if placed on a horizontal surface. When we push the wedge with a constant force, the block moves up the wedge. Find the work done by the external agent when the block has a speed v and is reaches the top of the wedge.
01:16View SolutionA block o plastic having a thin air cavity (whose thickenss is comparable to wavelength of light waves) is shown in fig. The thickness of air cavity (which can be considered as air wedge for interference pattern) is varying linearly from one end to other as shown. A broad beam of monochromatic light is incident normally from the top of the plastic box. Some ligth lis reflected back above and below the cavity .The plastic layers than wavelength of incident light . An observer when looking down from top sees an interference pattern consisting of eight dark fringes and seven bright fringe along the wedge. Take wavelength of incident light in air as lambda_(0) and refractive index of plastic as mu Assume that the thickness of the ends of air cavity are such that formation of fringe takes place there. Determine of difference L_(1) - L_(2) = Delta L) in terms of lambda_(0) .
04:51View SolutionA block o plastic having a thin air cavity (whose thickenss is comparable to wavelength of light waves) is shown in fig. The thickness of air cavity (which can be considered as air wedge for interference pattern) is varying linearly from one end to other as shown. A broad beam of monochromatic light is incident normally from the top of the plastic box. Some ligth lis reflected back above and below the cavity .The plastic layers than wavelength of incident light . An observer when looking down from top sees an interference pattern consisting of eight dark fringes and seven bright fringe along the wedge. Take wavelength of incident light in air as lambda_(0) and refractive index of plastic as mu Assume that the thickness of the ends of air cavity are such that formation of fringe takes place there. Determine the distance of 4th dark fringe from the left end of air cavity.
View SolutionA block o plastic having a thin air cavity (whose thickenss is comparable to wavelength of light waves) is shown in fig. The thickness of air cavity (which can be considered as air wedge for interference pattern) is varying linearly from one end to other as shown.
A broad beam of monochromatic light is incident normally from the top of the plastic box. Some ligth lis reflected back above and below the cavity .The plastic layers than wavelength of incident light . An observer when looking down from top sees an interference pattern consisting of eight dark fringes and seven bright fringe along the wedge. Take wavelength of incident light in air as λ0 and refractive index of plastic as μ
Assume that the thickness of the ends of air cavity are such that formation of fringe takes place there.

Determine the separation between 1st and 2nd dark fringes form the left end of air cavityView SolutionAll surfaces are smooth Find the horizontal displacements of the block and the wedge when the block slides down from top to bottom
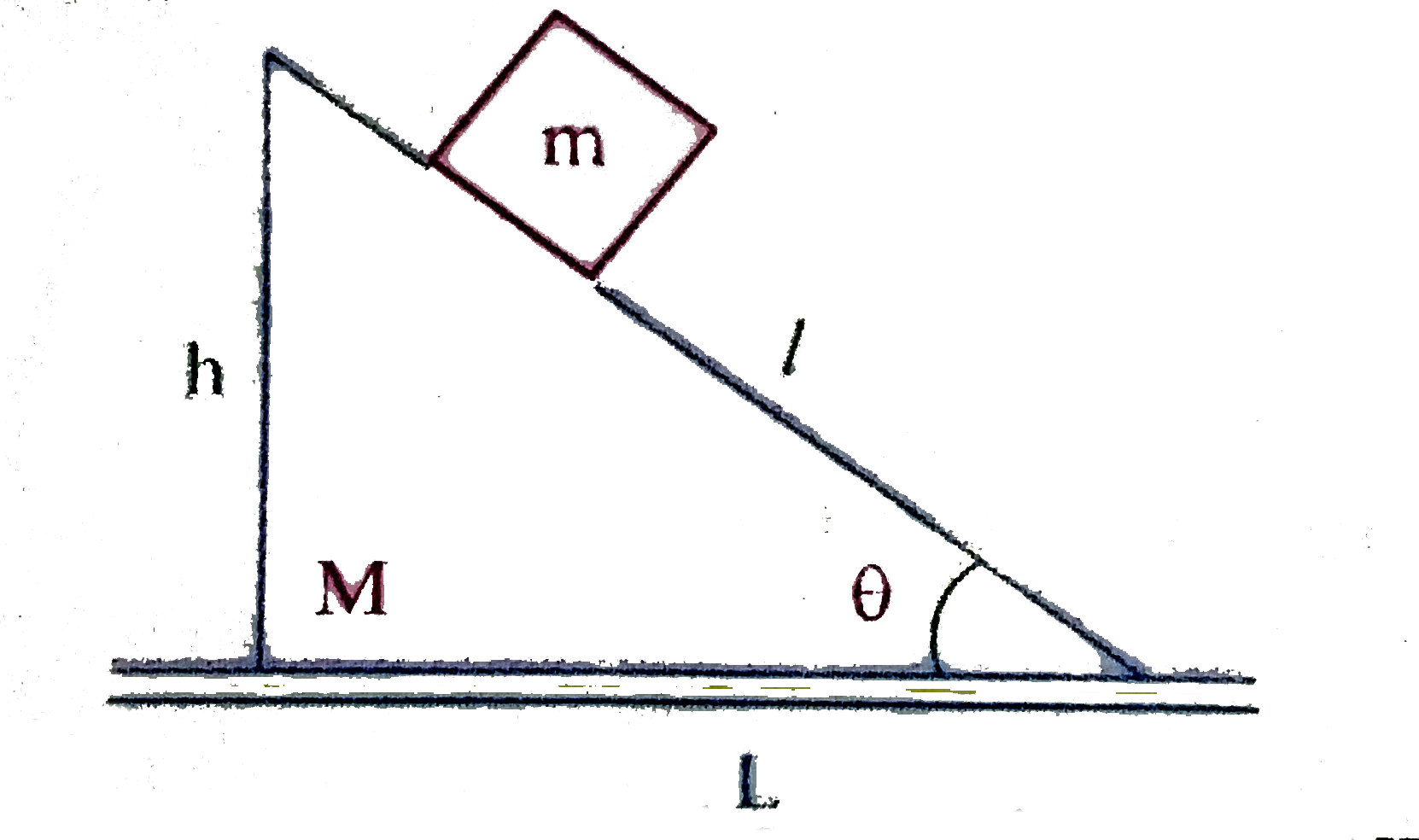 .17:27View Solution
.17:27View SolutionA block of mass m is placed at the top of a smooth wedge ABC. The wedge is rotated about an axis passing through C as shown in the figure - 3.81. The minimum value of angular speed ω such that the block does not slip on the wedge is :
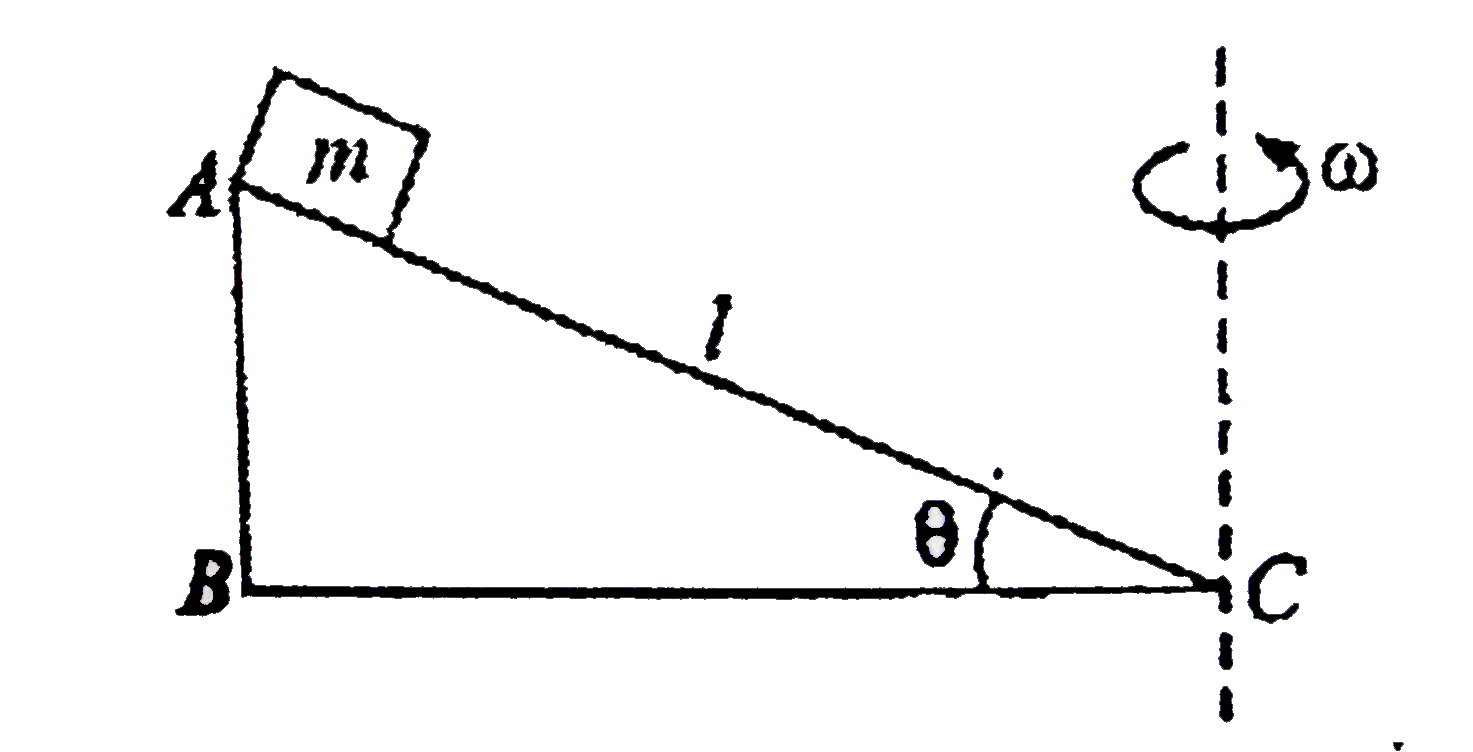 View Solution
View SolutionA parallel beam of white light is reflected from a thin wedge shaped film. The colour of the fringe at the edge of the wedge will be
View SolutionAll surfaces are smooth. Find the horizontal displacements of the block and wedge when the block slides down from top to bottom.
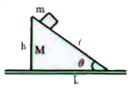 04:47View Solution
04:47View Solutionवायु से काँच की सिल्ली (अपवर्तनांक n, मोटाई d) पर θ कोण पर आपतित होने वाली एक प्रकाश किरण पर विचार कीजिए। काँच के शीर्ष पृष्ठ तथा तली के पृष्ठ परावर्तित होने वाली किरणों के बीच कलान्तर है
01:41View SolutionAll surfaces are smooth. Find the horizontal displacements of the block and wedge when the block slides down from top to bottom.
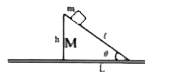 03:46View Solution
03:46View SolutionA block of mass 'M' is placed on the top of a wedge of mass '4M'. All the surfaces are frictionless. The system is released from rest. The distance moved by the wedge at the instant, the block reaches the bottom will be
 06:46View Solution
06:46View Solution

