Light of wavelength 620 nm passes through a double slit, yielding a diffraction pattern whose graph of intensity l versus angular position θ is shown in Figure. Calculate (a) the slit width and (b) the slit separation. (c) Verify the displayed intensities of thc m = 1 and m = 2 interference fringes.
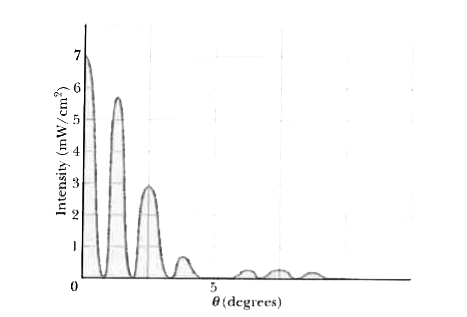
(a) 7.1 μm, (b) 28 μm, (c) for m=1, I=5.7mW/cm2, for m = 2, I=2.9mW/cm2
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION Book:RESNICK AND HALLIDAYChapter:INTERFERENCE AND DIFFRACTION Exercise:PRACTICE QUESTIONS (Single Correct Choice Type)
Explore 66 Videos
- INTERFERENCE AND DIFFRACTION Book:RESNICK AND HALLIDAYChapter:INTERFERENCE AND DIFFRACTION Exercise:PRACTICE QUESTIONS (More than One Correct Choice Type)
Explore 23 Videos
- INTERFERENCE AND DIFFRACTION Book:RESNICK AND HALLIDAYChapter:INTERFERENCE AND DIFFRACTION Exercise:CHECKPOINT
Explore 6 Videos
- HYDROGEN ATOMBook:RESNICK AND HALLIDAYChapter:HYDROGEN ATOMExercise:PRACTICE QUESTIONS(Integer Type)
Explore 6 Videos
- MAGNETIC FIELDS DUE TO CURRENTSBook:RESNICK AND HALLIDAYChapter:MAGNETIC FIELDS DUE TO CURRENTSExercise:Practice Question (Integer Type)
Explore 4 Videos
Similar Questions
Light of wavelength 520nm passing through a double slit,produced interference pattern of relative intensity versus deflection angle θ as shown in the figure.find the separation of between the slits.
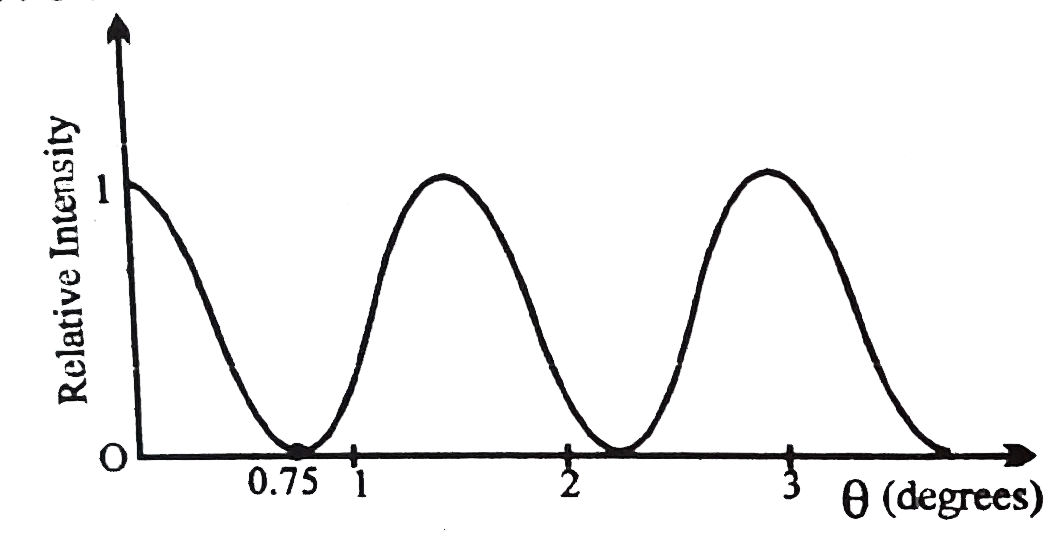
View SolutionLight of wavelength 520nm passing through a double slit,produced interference pattern of relative intensity versus deflection angle θ as shown in the figure.find the separation of between the slits.

View Solution
Knowledge Check
light of wavelength 600 nm is incident on a single slit. The first minimum of athe diffraction pattern is obtained at a distance of 4 m m from the centre. The distance between the screen and the slit is 2 m . What is the width of the slit ?
A0 . 1 m mB0 . 3 m mC0 . 5 mD0 . 6m mIf the intensity of light in double slit experiment from slit 1 and slit 2 are l0 and 25l0 respectively, find the ratio of intensities of light at minima and maxima in the interference pattern.
A0B49C2426D46
Light of wavelength 500 nm falls normally on a slit of width 1μm producing Fraunhofer diffraction pattern on a screen. Calculate the angular position of the first minimum and the angular width of the central maximum.
View SolutionIn young's double slit experiment relative intensity at a point on the screen may be defined as ratio of intensity at that point to the maximum intensity on the screen. Light of wavelength 7500∘A A passing through a double slit, produces interference pattern of relative intensity variation as shown in Fig. θ on horizontal axis represents the angular position of a point on the screen
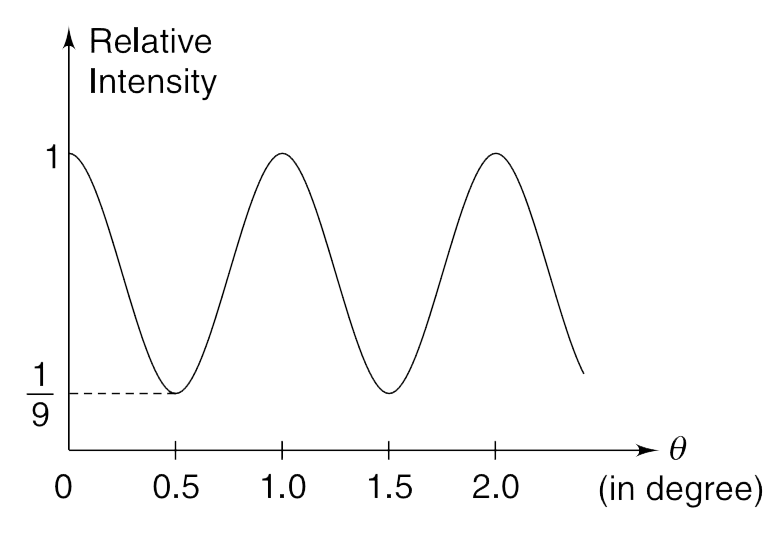
(a) Find separation d between the slits.
(b) Find the ratio of amplitudes of the two waves producing interference pattern on the screen.
View SolutionIn a single-slit diffraction experiment, light of wavelength λ illuminates the slit of width 'a' and the diffraction pattern is observed on a screen.
(a) Show the intensity distribution in the pattern with the angular position θ.
(b) How are the intensity and angular width of central maxima affected when
(i) width of slit is increased, and
(ii) separation between slit and screen is decreased ?
View SolutionIf the intensity of light in double slit experiment from slit 1 and slit 2 are l0 and 25l0 respectively, find the ratio of intensities of light at minima and maxima in the interference pattern.
View SolutionLight of wavelength 580 nm is incident on a slit having a width of 0.300 nm The viewing screen is 2.00 m from the slit. Find the positions of the first dark fringe and the width of the central bright fringe.
View SolutionLight of wavelength 6000Å is incident on a slit of width 0.30 mm. The screen is placed 2 m from the slit. Find (a) the position of the first dark fringe and (b). The width of the central bright fringe.
View Solution
