The mass of a muon is 207 times the electron mass, the average lifetime of muons at rest is 2.20 μs. In a certain experiment, muons moving through a laboratory are measured to have an average lifetime of 6.90 μs. For the moving muons, what are (a) β, (b) K, and (c ) p (in MeV/c)?
The correct Answer is:(a) 0.948; (b) 226 MeV; (c ) 314 MeV/c
Topper's Solved these Questions
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Single Corrrect Choice Type)
31 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Linked Comprehension)
11 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - CHECKPOINT
2 Videos
- PHOTONS AND MATTER WAVESBOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)
4 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))
3 Videos
Similar Questions
Mu on (μ−) is a negatively charged (|q|=|e|) particle with a mas mμ=200me where me is the mass of the electron and e is the electronic charge . If μ− is bound to a proton to from a hgydrogen like atom identify the correct statements
(A) Radius of the muonic orbit is 200 times smaller than that of the electron
(B) The speed of the μ− in the nth orbit is 1200 times that of the electron in the nth orbit
(c )The ionizaion energy of muonic atom is 200 times more than that of an hydrogen atom
(D) The momentum of the muon in the mth orbit is 200 times more than that of the electron
View SolutionMu on (μ−) is a negatively charged (|q|=|e|) particle with a mas mμ=200me where me is the mass of the electron and e is the electronic charge . If μ− is bound to a proton to from a hgydrogen like atom identify the correct statements
(A) Radius of the muonic orbit is 200 times smaller than that of the electron
(B) The speed of the μ− in the nth orbit is 1200 times that of the electron in the nth orbit
(c )The ionizaion energy of muonic atom is 200 times more than that of an hydrogen atom
(D) The momentum of the muon in the mth orbit is 200 times more than that of the electron
View Solution
Knowledge Check
The proper mean lifetime of a muon is 2.2×10−6s. A beam of muons is moving with speed 0.6c relative to an inertial observer. How far will a muon in the beam travel, on average, before it decays?
A288mB500mC360mD600mA meson when at rest decays 2 μs after it is created. If moving in the laboratory at 0.99c, its lifetime according to laboratory clocks would be
Athe sameB0.28 sC14 μsD4.6 s
The position verus time graph time graph for a certain particle moving along the x-axis is shown in . Find the average velocity in the time intervals (a) 0 to 2s, (b) 2s to 4s, and (c) 4,s to 7s,
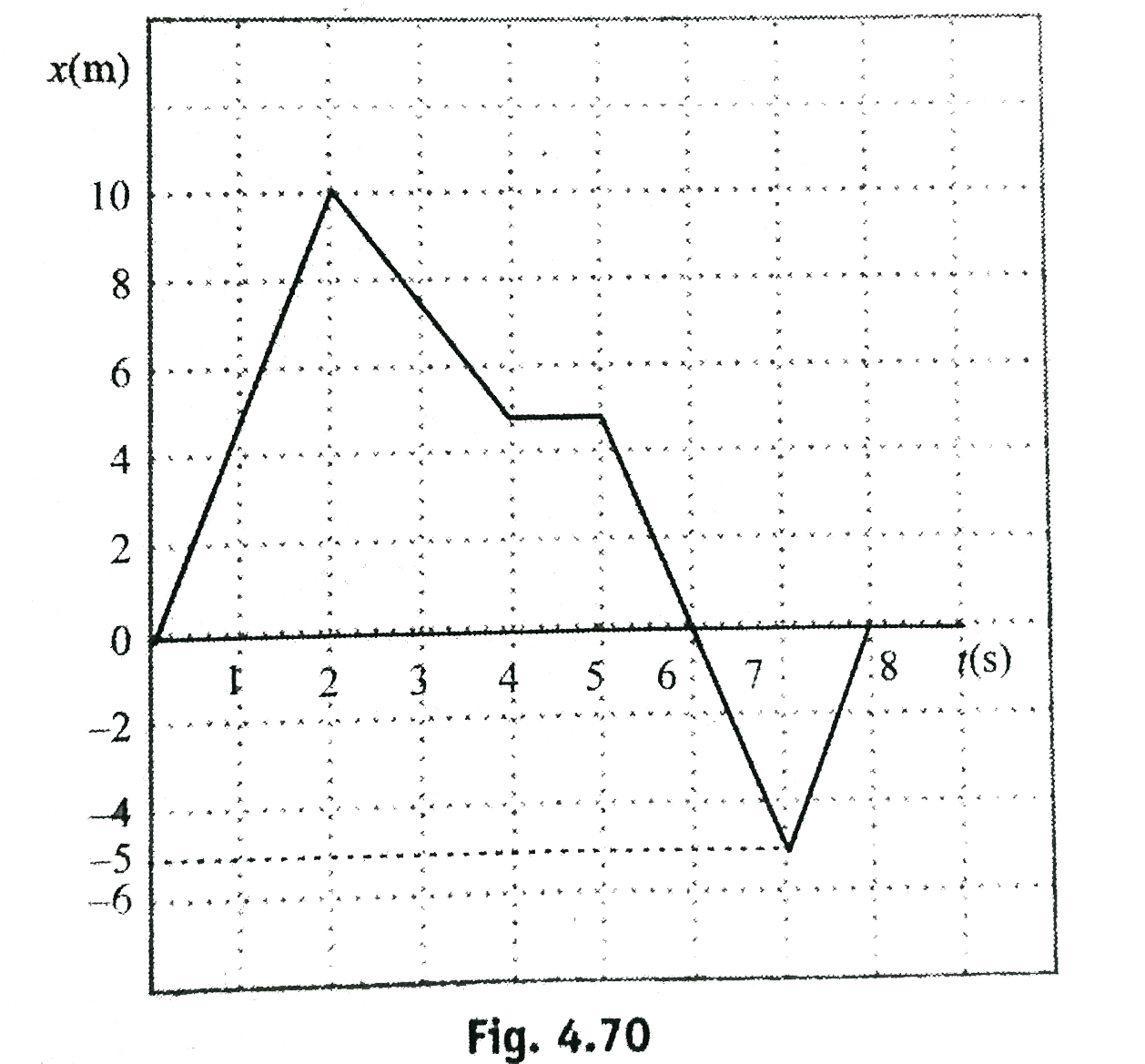 .
.
View SolutionThe position verus time graph time graph for a certain particle moving along the x-axis is shown in . Find the average velocity in the time intervals (a) 0 to 2s, (b) 2s to 4s, and (c) 4,s to 7s,
 .
.
View SolutionThe mean lifetime of stationary muons is measured to be 2.2000 μs. The mean lifetime of high-speed muons in a burst of cosmic rays observed from Earth is measured to be 20.000 μs. To five significant figures, what is the speed parameter β of these cosmic-ray muons relative to Earth?
View SolutionImagine that the electron in a hydrogen atom is replaced by a muon (μ). The mass of Muon particle is 207 times that of an electon and charge is equal to the charge of an electron. The ionization potential of this hydrogen atom will be:
View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
A formula analogous to Balmer's formula applies to the series of spectral lines which arise from transition from higher energy levels to the lowest energy level of hydrogen atom. Write this formula and use it to determine the ground state energy of a hydrogen atom in eV.
A 'muonic hydrogen atom' is like a hydrogen atom in which the electron is replaced by a heavier particle, the muon. The mass of a muon is about 207 times the mass of an electron, while its charge is the same as that of an electron. A muon has a very short lifetime, but we ignore its ubstable nature here.
View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
A formula analogous to Balmer's formula applies to the series of spectral lines which arise from transition from higher energy levels to the lowest energy level of hydrogen atom. Write this formula and use it to determine the ground state energy of a hydrogen atom in eV.
A 'muonic hydrogen atom' is like a hydrogen atom in which the electron is replaced by a heavier particle, the muon. The mass of a muon is about 207 times the mass of an electron, while its charge is the same as that of an electron. A muon has a very short lifetime, but we ignore its ubstable nature here.
View Solution
