The mean lifetime of stationary muons is measured to be 2.2000 . The mean lifetime of high-speed muons in a burst of cosmic rays observed from Earth is measured to be 20.000 . To five significant figures, what is the speed parameter of these cosmic-ray muons relative to Earth?
The correct Answer is:0.993 93
Topper's Solved these Questions
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Single Corrrect Choice Type)
31 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Linked Comprehension)
11 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - CHECKPOINT
2 Videos
- PHOTONS AND MATTER WAVESBOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)
4 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))
3 Videos
Similar Questions
The length of a spaceship is measured to be 25% of its rest length. (a) To three significant figures, what is the speed parameter β of the spaceship relative to the observer's frame? (b) By what factor do the spaceship's clocks run slow relative to clocks in the observer's frame?
View SolutionThe elementary particle known as the positive kaon (K+) is unstable in that it can decay (transform) into other particles. Although the decay occurs randomly, we find that, on average, a positive kaon has a lifetime of 0.1237 μs when stationary-that is, when the lifetime is measured in the rest frame of the kaon. If a positive kaon has a speed of 0.990c relative to a laboratory reference frame when the kaon is produced, how far can it travel in that frame during its lifetime according to classical physics (which is a reasonable approximation for speeds much less than c) and according to special relativity (which is correct for all physically possible speeds)?
View Solution
Knowledge Check
The proper mean lifetime of a muon is 2.2×10−6s. A beam of muons is moving with speed 0.6c relative to an inertial observer. How far will a muon in the beam travel, on average, before it decays?
A288mB500mC360mD600mParagraph : A spaceship traveling east flies directly over the head of an inertial observer who is at rest on the Earth's surface. The speed of the spaceship can be found from this relationship: √1−v2/c2=1/2.
The pilot fires an ion gun that propels ions from the space ship at 1.0×108m/s relative to the ship. What is the speed of the ions as measured by the Earth observer?A1.0×108m/sB2.4×108m/sC2.0×108m/sD2.8×108m/s
Consider the neutron capture reaction
109Ag+n→110A>o110Ag+γ (40-34)
in which a compound nucleus (110Ag) is formed. Figure 40-18 shows the relative rate at which such events take place, plotted against the energy of the incoming neutron. Find the mean lifetime of this compound nucleus by using the uncertainty principle in the form
ΔE.Δt≈ˆh. (40-35)
here ΔE is a mesure of the uncertainty with which the energy of a state can be defined. The quantity Δt is a measure of the time available of measure this energy. In fact here Δt is just tavg, the average life of the compound nucleus befoe it decays to its ground state.
Reasoning: We see that the relative reaction rate peaks sharply at a neutron energy of about 5.2 eV.This suggests that we are dealing with a single excited energy level of the compund nucleus 110Ag. When the availabel energy(of the incoming neutron) just matches the energy of this level above the neutron) just matches the energy of this level above the 110Ag ground state, we have resonance and the reaction of Eq. 40 -34 really goes.
However, the resonance peak is not infinitely sharp but has an approximate half peak is not infinitely shart but has an approximate half width (ΔE in the figue) of about 0.20 eV. We can account for this resonance peak width by saying that the excited level is not sharply defined in energy but has an energy uncertainty ΔE of about 0.20 eV.
Calculation : Subsitiuting that uncertainty of 0.20 2V into Eq. given us
Δ=tavg≈hΔE≈(4.14×10−15eV.s)/2π0.20eV
≈3×10−15s.
This is several hundraed times greater than the time a 5.2 eV neutron takes to cross the diameter of a 109Ag nucleus . Therefore , the neutron is spending this time of 3×10−15 s as part of the nucleus.
View SolutionThe mass of a muon is 207 times the electron mass, the average lifetime of muons at rest is 2.20 μs. In a certain experiment, muons moving through a laboratory are measured to have an average lifetime of 6.90 μs. For the moving muons, what are (a) β, (b) K, and (c ) p (in MeV/c)?
View Solution(Come) back to the future. Suppose that a father is 25.0 y older than his daughter. He wants to travel outward from Earth for 2.000 y and then back for another 2.000 y (both intervals as he measures them) such that he is then 25.0 y younger than his daughter. What constant speed parameter β(relative to Earth) is required ?
View SolutionEarth's lower atmosphere contains negative and positive ions that are produced by radioactive elements in the soil and cosmic rays from space. In a certain region, the atmospheric electric field strength is 120 V/m and the field is directed vertically down. This field causes singly charged positive ions, at a density of 640cm−1 to drift downward and singly charged negative ions, at a density of 550 cm−3. ? to drift upward (Fig. 26-20). The measured conductivity of the air in that region is 2.70×10−14W(Ω.m)−1. Calculate (a) the magnitude of the current densily and (b) the ion drift speed, assumed to be the same for positive and negative ions.
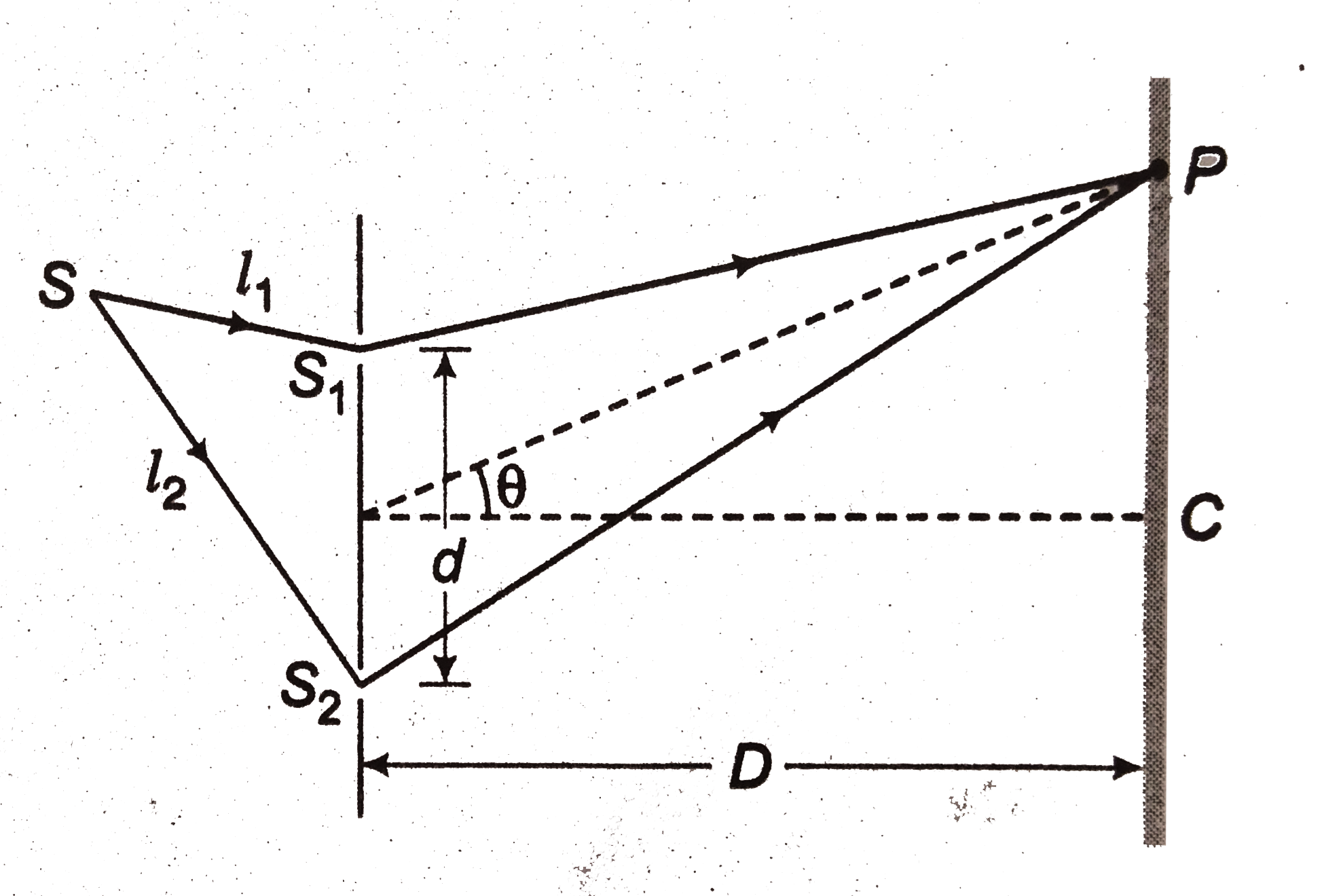
View SolutionIn a Young's double slit experiment, the light sources is at distance l1=20μm and l2=40μm form the main slit. The light of wavelength lambda = 500nm is incident on slits separated at a distance 10μm. A screen is placed at a distance D = 2 away from the slits as shown in figure. Find
(a) the values of θ relative to the central line where maxima appear on the screen?
(b) how many maxima will appear on the screen?
what should be the minimum thickness of a slab of refractive index 1.5 placed on the path of one of the ray so that minima occurs at C ?
 .
.
View SolutionEinstein in 1905 proppunded the special theory of relativity and in 1915 proposed the general theory of relativity. The special theory deals with inertial frames of reference. The general theory of relativity deals with problems in which one frame of reference. He assumed that fixed frame is accelerated w.r.t. another frame of reference of reference cannot be located. Postulated of special theory of realtivity
● The laws of physics have the same form in all inertial systems.
● The velocity light in empty space is a unicersal constant the same for all observers.
● Einstein proved the following facts based on his theory of special relativity. Let v be the velocity of the speceship w.r.t a given frame of reference. The obserations are made by an observer in that reference frame.
● All clocks on the spaceship wil go slow by a factor √1−v2/c2
● All objects on the spaceship will have contracted in length by a factor √1−v2/c2
● The mass of the spaceship increases by a factor √1−v2/c2
● Mass and energy are interconvertable E=mc2
The speed of a meterial object can never exceed the velocity of light.
● If two objects A and B are moving with velocity u and v w.r.t each other along the x-axis, the relative velocity of A w.r.t. B=u−v1−uv/v2
One cosmic ray particle appraches the earth along its axis with a velocity of 0.9c towards the north the and another one with a velocity of 0.5c towards the south pole. The relative speed of approcach of one particle w.r.t. another is-
View Solution
