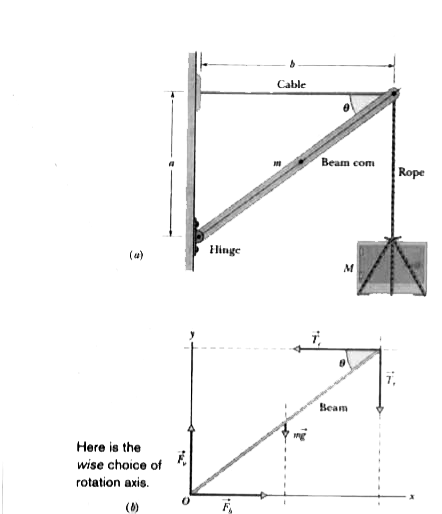
Figure 11-16a shows a safe (mass M = 430 kg) hanging by a rope (negligible mass) from a boom (a = 1.9 m and b = 2.5 m) that consists of a uniform hinged beam (m=85 kg) and horizontal cable (negligible mass).
What is the tension Tc in the cable? In other words, what is the magnitude of the force →Tc on the beam from the cable?
The system here is the beam alone, and the forces on it are shown in the free-body diagram. The force from the cable is →Tc. The gravitational force on the beam acts at the bcam.s center of mass (at the heam.s center) and is represented by its equivalent m→g. The vertical component of the force on the beam from the hinge is →Fv and the horizontal component of the force from the hinge is →Fh. The force from the rope supporting the safe is →Tr. Because beam, rope, and safe are stationary, the magnitude of →Tr is equal to the weight of the safe: Tr=Mg. We place the origin O of an xy coordinate system at the hinge. Because the system is in static equilibrium, the balancing equations apply to it.
calculation: let us start with Eq. 11-27(τnet,z=0) Note that we are asked for the magnitude of force →Tc and not of forces →Fh and →Fv acting at the hinge, at point O. To eliminate →Fh and →Fv from the torque calculation, we should calculate torques about an axis that is perpendicular to the figure at point O. Then →Fh and →Fv will have moment arms of zero. The lines of action for →Tc→Tr, and m→g are dashed. The corresponding moment arms are a, b, and b/2.
Writing torques in the form of r⊥F and using our rule about signs for torques, the balancing equation τnet,z=0 becomes
(a)(Tc)−(b)(Tr)−(12b)(mg)=0(11-29)
Substituting Mg for Tr and solving for Tc we find that
Tc=gb(M+12m)a
(9.8m/s2)(2.5m)(430kg+852kg)1.9m
=6093N≈6100N.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - EXAMPLE1videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - CHECKPOINT4videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))3videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)4videos
TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION
Similar Questions
Figure 11-16a shows a safe (mass M = 430 kg) hanging by a rope (negligible mass) from a boom (a = 1.9 m and b = 2.5 m) that consists of a uniform hinged beam (m=85 kg) and horizontal cable (negligible mass).
Find the magnitude F of the net force on the beam from the hinge.View SolutionFor the uniform 5 kg beam shown in figure-2.41(a), how large is the tension in the supporting cable and what are the components of the force exerted by the hinge on the beam ? Take g=10m/s2
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The mass of a lift is 600 kg and it is moving upwards with a uniform acceleration of 2m/s2. Then the tension in the cable of the lift is-
A7080 NB5880 NC4680 NDzero N - Question 2 - Select One
The mass of a lift if 600kg and it is moving upwards with a uniform acceleration of 2m/s2. Then the tension in the cable of the lift is :
A7200 NB5900 NC4700 NDzero N - Question 3 - Select One
A rope of length 4 m having mass 1.5 kg/m lying on a horizontal frictionless surface is pulled at one end by a force of 12N. What is the tension in the rope at a point 1.6 m from the other end?
A5NB4.8NC7.2ND6N
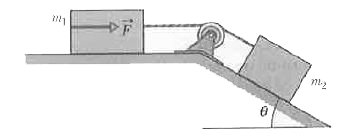
Figure 5-59 shows a box of mass m2=1.0 kg on a friction-less plane inclined at angle θ=30∘. It is connected by a cord of negligible mass to a mass m1=2.5 kg on a horizontal frictionless surface. The pulley is frictionless and massless. (a) If the magnitude of horizontal force →F is 2.3 N, what is the tension in the connecting cord? (b) What is the largest value the magnitude of →F may have without the cord becoming slack?
 View Solution
View SolutionThe mass of a lift if 600kg and it is moving upwards with a uniform acceleration of 2m/s2. Then the tension in the cable of the lift is :
View SolutionIn figure the uniform gate weights 300N and is 3m wide &2m high. It is supported by a hinge at the bottom left corner and a horizontal cable at the top left corner, as shown. Find :
(a) the tension in the cable and
(b) the force that the hinge exerts on the gate ( magnitude & direction ).
 View Solution
View SolutionIn figure the uniform gate weights 300N and is 3m wide &2m high. It is supported by a hinge at the bottom left corner and a horizontal cable at the top left corner, as shown. Find :
(a) the tension in the cable and
(b) the force that the hinge exerts on the gate ( magnitude & direction ).
 View Solution
View SolutionFigure 5-50 shows two blocks connected by a cord (of negligible mass) that passes over a frictionless pulley (also of negligible mass). The arrangement is known as Atwood's machine. One block has mass m1=1.30 kg, the other has mass m2=2.80 kg. What are (a) the magnitude of the blocks' acceleration and (b) the tension in the cord ?
 View Solution
View Solution

