a ladder of length L=12 m and mass m = 45 kg leans against a slick wall (that is, there is no friction between the ladder and the wall). The ladder's upper end is at height h = 9.3 m above the pavement on which the lower end is supported (the pavement is not frictionless). The ladder's center of mass is L/3 from the lower end, along the length of the ladder. A firefighter of mass M = 72 kg climbs the ladder until her center of mass is L/2 from the lower end. What then are the magnitudes of the forces on the ladder from the wall and the pavement?
To solve the problem of the ladder leaning against a slick wall with a firefighter climbing it, we will follow these steps:
Step 1: Understand the System
We have a ladder of length L=12m and mass m=45kg leaning against a slick wall. The height of the top of the ladder from the ground is h=9.3m. A firefighter of mass M=72kg climbs the ladder until her center of mass is L/2 from the lower end.
Step 2: Determine the Geometry
Using the Pythagorean theorem, we can find the base of the ladder (b):
b=√L2−h2=√122−9.32=√144−86.49=√57.51≈7.58m
Step 3: Identify Forces Acting on the Ladder
1. The weight of the ladder Wl=mg=45×9.8=441N acting downwards at L/3 from the bottom.
2. The weight of the firefighter Wf=Mg=72×9.8=705.6N acting downwards at L/2 from the bottom.
3. The normal force from the wall R1 acting horizontally at the top of the ladder.
4. The normal force from the pavement R2 acting vertically upwards at the bottom of the ladder.
5. The friction force F acting horizontally at the bottom of the ladder.
Step 4: Set Up the Equations
Sum of Forces in the Horizontal Direction:
R1−F=0(1)
Sum of Forces in the Vertical Direction:
R2−Wl−Wf=0(2)
Taking Moments about the Bottom of the Ladder:
The torque about the bottom of the ladder must be zero for equilibrium:
Wl⋅L3⋅cos(θ)+Wf⋅L2⋅cos(θ)−R1⋅L⋅sin(θ)=0(3)
Step 5: Calculate Angles and Trigonometric Functions
Using the height and base calculated earlier:
sin(θ)=hL=9.312≈0.775
cos(θ)=bL=7.5812≈0.632
Step 6: Substitute Values into the Torque Equation
Substituting the values into equation (3):
441⋅123⋅0.632+705.6⋅122⋅0.632−R1⋅12⋅0.775=0
Calculating each term:
441⋅4⋅0.632+705.6⋅6⋅0.632−12R1⋅0.775=0
1117.248+2671.488−9.3R1=0
3788.736=9.3R1⟹R1≈407.4N
Step 7: Calculate R2
Using equation (2):
R2=Wl+Wf=441+705.6=1146.6N
Final Step: Round the Results
Rounding to significant figures:
- R1≈410N
- R2≈1100N
Summary of Results
The magnitudes of the forces on the ladder are:
- Force from the wall R1≈410N
- Force from the pavement R2≈1100N
We have a ladder of length L=12m and mass m=45kg leaning against a slick wall. The height of the top of the ladder from the ground is h=9.3m. A firefighter of mass M=72kg climbs the ladder until her center of mass is L/2 from the lower end.
Using the Pythagorean theorem, we can find the base of the ladder (b):
b=√L2−h2=√122−9.32=√144−86.49=√57.51≈7.58m
1. The weight of the ladder Wl=mg=45×9.8=441N acting downwards at L/3 from the bottom.
2. The weight of the firefighter Wf=Mg=72×9.8=705.6N acting downwards at L/2 from the bottom.
3. The normal force from the wall R1 acting horizontally at the top of the ladder.
4. The normal force from the pavement R2 acting vertically upwards at the bottom of the ladder.
5. The friction force F acting horizontally at the bottom of the ladder.
Sum of Forces in the Horizontal Direction:
R1−F=0(1)
R2−Wl−Wf=0(2)
The torque about the bottom of the ladder must be zero for equilibrium:
Wl⋅L3⋅cos(θ)+Wf⋅L2⋅cos(θ)−R1⋅L⋅sin(θ)=0(3)
Using the height and base calculated earlier:
sin(θ)=hL=9.312≈0.775
cos(θ)=bL=7.5812≈0.632
Substituting the values into equation (3):
441⋅123⋅0.632+705.6⋅122⋅0.632−R1⋅12⋅0.775=0
Calculating each term:
441⋅4⋅0.632+705.6⋅6⋅0.632−12R1⋅0.775=0
1117.248+2671.488−9.3R1=0
3788.736=9.3R1⟹R1≈407.4N
Using equation (2):
R2=Wl+Wf=441+705.6=1146.6N
Rounding to significant figures:
- R1≈410N
- R2≈1100N
The magnitudes of the forces on the ladder are:
- Force from the wall R1≈410N
- Force from the pavement R2≈1100N
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - EXAMPLE1videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - CHECKPOINT4videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))3videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)4videos
TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION
Similar Questions
Knowledge Check
- Question 1 - Select One
A ladder of length l and mass m is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is μ. The angle θ at which the ladder will stay in equilibrium is
Aθ=tan−1(μ)Bθ=tan−1(2μ)Cθ=tan−1(μ2)Dnone of these - Question 2 - Select One
A ladder of mass 10kg is held at reat against a smooth wall on a rough ground as shown in figure. The normal reaction between the wall and the ladder is
 A50NB50√3NC60√3ND100N
A50NB50√3NC60√3ND100N - Question 3 - Select One
The mass of a uniform ladder of length 5m is 20kg. A person of mass 60kg stand on the ladder at a height of 2m from the bottom. The position of centre of mass of the ladder and man from the bottom is
A1.256mB2.532mC3.513mD2.125m
A uniform ladder of length 3.25 m and weight 250 N is placed against a smooth vertical wall with its lower end 1.25 m from the wall. If coefficient of friction between the ladder and the floor is 0.3, then, find the frictional force acting on the ladder at the point of contact between ladder and floor.
View SolutionA ladder leaning against a wall makes an angle of 60o with the ground. If the length of the ladder is 19 m, find the distance of the foot of the ladder from the wall.
View SolutionA ladder 10m long is leaning against a vertical wall, it makes an angle of 60° with the ground.How far is the foot of the ladder from the wall?
View SolutionA 15-m long ladder is placed against a wall to reach a window 12 m high.Find the distance of the ladder from the wall.
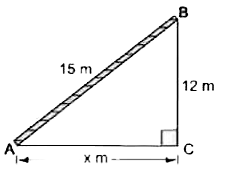 View Solution
View SolutionA ladder of length 5m is placed against a smooth wall as shown in figure. The coefficient or friction is μ between ladder and ground. What is the minimum value of μ , If the ladder is not to slip?
 View Solution
View Solution

