Question

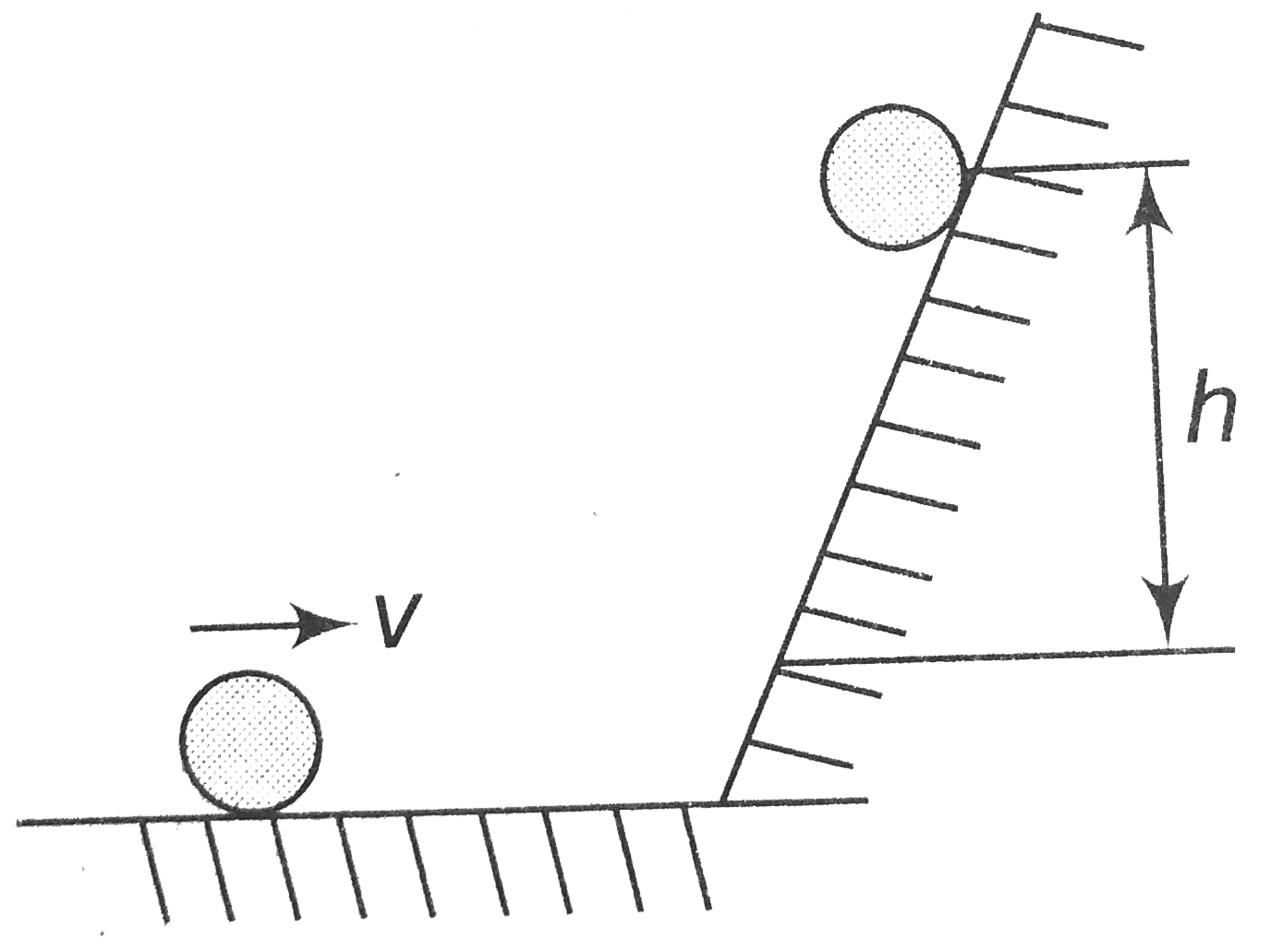
Disks A and B are identical and roll across a floor with equal speeds. Then disk A rolls up an incline, reaching a maximum height h, and disk B moves up an incline that is identical except that it is frictionless. Is the maximum height reached by disk B greater than, less than, or equal to h?

Explanation

To solve the problem, we will use the principle of conservation of energy for both disks A and B.

Step 1: Understand the initial conditions
Both disks A and B are rolling with the same initial speed \( V \) on a flat surface before they start ascending their respective inclines.

Step 2: Analyze Disk A
Disk A rolls up an incline with friction. The total mechanical energy at the bottom (initial position) consists of translational kinetic energy and rotational kinetic energy:
- Translational kinetic energy: \( KE_{trans} = \frac{1}{2} m V^2 \)
- Rotational kinetic energy: \( KE_{rot} = \frac{1}{2} I \omega^2 \)

For a disk, the moment of inertia \( I \) is given by \( I = \frac{1}{2} m r^2 \) and the relationship between linear velocity \( V \) and angular velocity \( \omega \) is \( V = r \omega \), which gives \( \omega = \frac{V}{r} \).

Substituting \( \omega \) in the rotational kinetic energy:
\( KE_{rot} = \frac{1}{2} \left(\frac{1}{2} m r^2\right) \left(\frac{V}{r}\right)^2 = \frac{1}{4} m V^2 \)

Thus, the total initial energy for disk A is:
\( E_{initial, A} = KE_{trans} + KE_{rot} = \frac{1}{2} m V^2 + \frac{1}{4} m V^2 = \frac{3}{4} m V^2 \)

As disk A rolls up the incline, it converts this energy into potential energy \( PE = mgh \) at the maximum height \( h \):
\( \frac{3}{4} m V^2 = mgh \)
Solving for \( h \):
\( h = \frac{3}{4} \frac{V^2}{g} \)

Step 3: Analyze Disk B
Disk B rolls up a frictionless incline. The initial energy is the same as disk A:
\( E_{initial, B} = \frac{3}{4} m V^2 \)

However, since there is no friction, the rotational kinetic energy remains unchanged as it rolls up the incline. At the maximum height, all the energy is converted into potential energy and rotational kinetic energy:
\( \frac{3}{4} m V^2 = mgh' + KE_{rot} \)
Where \( h' \) is the maximum height reached by disk B. The rotational kinetic energy remains:
\( KE_{rot} = \frac{1}{4} m V^2 \)
Thus, we have:
\( \frac{3}{4} m V^2 = mgh' + \frac{1}{4} m V^2 \)
Rearranging gives:
\( \frac{3}{4} m V^2 - \frac{1}{4} m V^2 = mgh' \)
\( \frac{2}{4} m V^2 = mgh' \implies \frac{1}{2} m V^2 = mgh' \)
Solving for \( h' \):
\( h' = \frac{1}{2} \frac{V^2}{g} \)

Step 4: Compare heights
Now we compare \( h' \) and \( h \):
- \( h = \frac{3}{4} \frac{V^2}{g} \)
- \( h' = \frac{1}{2} \frac{V^2}{g} \)

Since \( \frac{3}{4} > \frac{1}{2} \), we conclude:
\( h' < h \)

Final Answer
The maximum height reached by disk B is less than the maximum height \( h \) reached by disk A.