Figure shows a mass m placed on a frictionless horizontal table and attached toa string passing through a mall hole in the surface. Initially, themas movesin a circle of radius with a speed and the ree end of the string is held by a person. The person pulls on the string slowly to decrease the radius of th circle of r. a. Find the tension in the string when the mass moves in the circle of radius r. b. Calculate the chasnge in the kinetic energy of the mass
The torque acting on the mass m about the vertical axis through the hole is zero. The angular momentum about this axis, therefore, remains constant. If the speed of the mass is v whenit moves in the circel of radius r we have
or .......i ltbr> a. the tension =1/2mv^2-1/2mv_0^2=1/2mv_0^2[r_0^2/r^2-1]
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:HC VERMAChapter:ROTATIONAL MECHANICSExercise:Short Answer
Explore 22 Videos
- ROTATIONAL MECHANICSBook:HC VERMAChapter:ROTATIONAL MECHANICSExercise:Objective 1
Explore 26 Videos
- ROTATIONAL MECHANICSBook:HC VERMAChapter:ROTATIONAL MECHANICSExercise:Exercises
Explore 86 Videos
- REST AND MOTION : KINEMATICSBook:HC VERMAChapter:REST AND MOTION : KINEMATICSExercise:Exercises
Explore 51 Videos
- SIMPLE HARMONIC MOTIONBook:HC VERMAChapter:SIMPLE HARMONIC MOTIONExercise:Exercises
Explore 58 Videos
Similar Questions
A small block of mass m on a horizontal smooth table is attached to a light string passing through a hole as shown in the figure. Initially, the block moves in a circle of radius r with speed v and the string is held by a person. The person pulls the strin slowly to decrease the radius of circle to r/2. (a) Find the tension in the string when the block moves in a circle of radius r/2. (b) Calculate the change in the kinetic energy of the block.

View SolutionAn air puck of mass m1 is tied to a string allowed to revolved in a circle of radius R on a frictionless horizontal table . The other end of the string passes through a small hole in the centre of the table , and a load of mass m2 is tied to the string? The suspended load remains in equilibrium while the pack on the tabletop revolves.

a. Find the tension in the string
b. Find the radial force acting on the puck
c. Find the speed of the puck
d. Qualitaively describe what will happen in the monsion of the puck if the value of m2 is somewhat increased by placing an additional load on it.
e.Qualitaively describe what will happen in the monsion of the puck if the value of m2 is instead decreased removing a part from the hanging load.
View Solution
Knowledge Check
A mass is supported on a frictionless horizontal surface. It Is attached to a string and rotates about a fixed center at an angular velocity ω0.If the length of the string and angular velocity both are doubled, the tension in the string which was initially T0 is now
AT0BT0/2C4T0D8T0A puck of mass m=50.0g is attached to a taut cord passing through a small hole in a frictionless, horizontal surface (Fig.) The puck is initially orbiting with speed vi=1.50m/s in a circle of radius ri=0.30m. The cord is then slowly pulled from below, decreasing the radius of the circle to r=0.10m. The puck's speed at the smaller radius is.
 .A2.25m/sB5.50m/sC4.50m/sD6.0m/s
.A2.25m/sB5.50m/sC4.50m/sD6.0m/sA point mass m is moved in vertical circle of radius r with help of string. Velocity of mass is 7gr√ at lowest point. Tension in string at lowest point is
A7 mgB8 mgC1 mgD6 mg
The mass of the part of the string below A i figure is m. Find the tension of he string at the lowere end and at A.
View SolutionA mass of 0.675 kg on a frictionless table is attached to a string which passes through a hole in the table at the centre. If the radius of the circle in which the mass rotates, is 5 m when its speed is 10ms−1, find the tension of the string. It is found that on drawing down the string by 0.2 m, the tension is increased 4.63 times. Calculate the work done by the string on the revolving mass during the reduction of the radius.
[Hint : Apply work-energy theorem to find work done by the force]
View SolutionA string of 7m length has a mass of 0.035kg. If tension in the string is 60.N, then speed of a wave on the string is
View SolutionA particle of mass m is rotated in a vertical circle by means of a string . The differnce in the tensions in the string at the bottom and the top of the circle would be
View SolutionA mass m moves in a circle on a smooth horizontal plane with velocity v0 at a radius R0. The mass is attached to a string which passes through a smooth hole in the plane as shown.
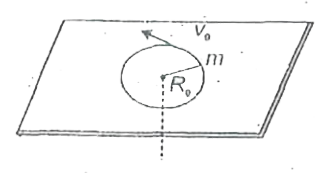
The tension in the string is increased gradually and finally m moves in a circle of radius R02. The final value of the kinetic energy is
View Solution
