If C1,C2,C3,C4 are the coefficients of any consecutive terms in the expansion of (1+x)n , prove that :
C1C1+C2+C3C3+C4=2C2C2+C3
Step by step video & image solution for If C_1, C_2 , C_3 , C_4 are the coefficients of any consecutive terms in the expansion of (1+x)^n , prove that : (C_1)/(C_1+C_2) + (C_3)/(C_3+C_4) = (2C_2)/(C_2 + C_3) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- BINOMIAL THEOREMBOOK - MODERN PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - CHECK YOUR UNDERSTANDING
10 Videos
- BINOMIAL THEOREMBOOK - MODERN PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - COMPETITION FILE (JEE MAIN)
11 Videos
- BINOMIAL THEOREMBOOK - MODERN PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - EXERCISE
9 Videos
- COMPLEX NUMBERSBOOK - MODERN PUBLICATIONCHAPTER - COMPLEX NUMBERSEXERCISE - CHAPTER TEST
12 Videos
Similar Questions
If C0,C1,C2,…,Cn are the binomial coefficients
in the expansion of (1+x)n , prove that
(C0+2C1+C2)(C1+2C2+C3)…(Cn−1+2Cn+Cn+1)
(n−2)n(n+1)!n∏r=1(Cr−1+Cr).
View SolutionIf C0,C1,C2,...Cn are the binomial coefficients in the expansion of (1+x)n then prove that: C0+C12+C23+……+Cnn+1=2n+1−1n+1
View Solution
Knowledge Check
If C0,C1,C2,…,Cn are the coefficients in the expansion of (1+x)n, then what is the value of C1+C2+C3+….+Cn ?
A2nB2n−1C2n−1D2n−2If C0,C1,C2,...,Cn are binomial coefficients
in the expansion of (1+x)n, then the value of
C0−C12+C23−C34+...+(−1)nCnn+1 isA0B1n+1C22n+1D−1n+1If C0,C1,C2,...,Cn denote the binomial coefficients in the expansion of (1+x)n , then .
1.C1−2.C2+3.C3−4.C4+...+(−1)n−1nCn=A0B2nCn2n−1D−n2n−1
If a. b, c and d are the coefficients of 2nd, 3rd, 4th and 5th terms respectively in the binomial expansion of (1+x)n, then prove that aa+b+cc+d=2bb+c
View SolutionIn C0,C1C2….Cn are the binomial coefficients in the expansion of (1+x)n then prove that :
(i)C20−C21+C22−C23+…..+(−1)n.C2n
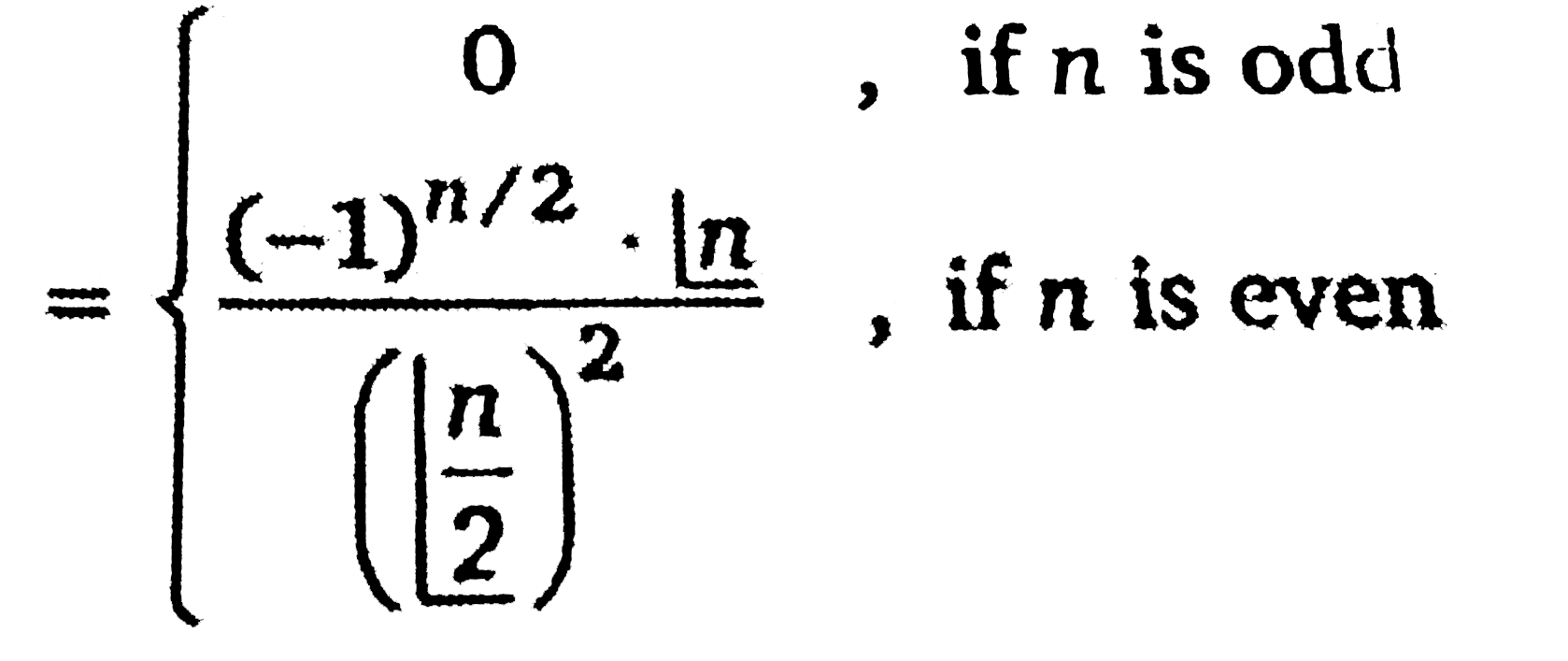
(ii)C0C1+C1C2+C2C3+....+Cn−1Cn
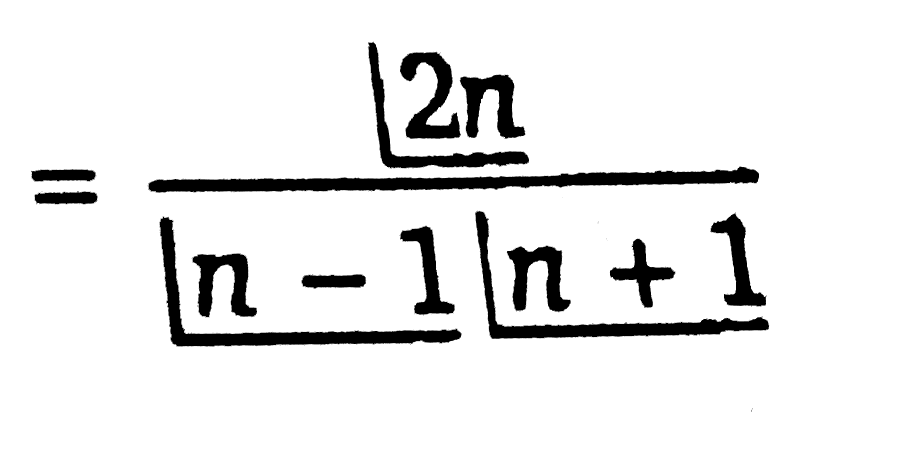
View SolutionIf C0,C1,C2,…C15 are the binomial coefficients in the expansion of (1+x)15, then
C1C0+2C2C1+3C3C2+…+15C15C14=
View SolutionIf C0,C1,C2,...,Cn denote the cefficients in the expansion of (1+x)n, then
C0+3.C1+5.C2+...+(2n+1)Cn= .
View SolutionIf C1,C2,C3,…Cn denote the coefficients in the binomial expansion of (1+x)n, then the value of nC1+2.nC2+3.nC3+….+n.nCn is
View Solution
