A body travels such that square of time is proportional to the displacement. Its acceleration is:
zero
infinite
constant
variable
The correct Answer is:C
To solve the problem, we need to analyze the relationship between time and displacement given in the question.
1. Understanding the Relationship:
We are given that the square of time (t²) is proportional to the displacement (s). This can be expressed mathematically as:
s∝t2
This means:
s=kt2
where k is a constant of proportionality.
2. Finding Velocity:
Velocity (v) is defined as the rate of change of displacement with respect to time. Mathematically, this is given by:
v=dsdt
To find v, we differentiate s=kt2 with respect to t:
v=ddt(kt2)=k⋅ddt(t2)=k⋅2t=2kt
3. Finding Acceleration:
Acceleration (a) is defined as the rate of change of velocity with respect to time. This can be expressed as:
a=dvdt
Now, we differentiate v=2kt with respect to t:
a=ddt(2kt)=2k⋅ddt(t)=2k⋅1=2k
4. Conclusion:
The acceleration a is a constant value, specifically 2k. Since k is a constant, the acceleration does not change over time.
Final Answer:
The acceleration of the body is a constant value 2k.
---
We are given that the square of time (t²) is proportional to the displacement (s). This can be expressed mathematically as:
s∝t2
This means:
s=kt2
where k is a constant of proportionality.
Velocity (v) is defined as the rate of change of displacement with respect to time. Mathematically, this is given by:
v=dsdt
To find v, we differentiate s=kt2 with respect to t:
v=ddt(kt2)=k⋅ddt(t2)=k⋅2t=2kt
Acceleration (a) is defined as the rate of change of velocity with respect to time. This can be expressed as:
a=dvdt
Now, we differentiate v=2kt with respect to t:
a=ddt(2kt)=2k⋅ddt(t)=2k⋅1=2k
The acceleration a is a constant value, specifically 2k. Since k is a constant, the acceleration does not change over time.
The acceleration of the body is a constant value 2k.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE ( C.(MULTIPLE CHOICE QUESTIONS))13videos
MOTION IN A STRAIGHT LINE
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE ( D.(MULTIPLE CHOICE QUESTIONS))9videos
MOTION IN A STRAIGHT LINE
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE ( A.(MULTIPLE CHOICE QUESTIONS))20videos
MOTION IN A STRAIGHT LINE
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test15videos
MOTION IN A PLANE
- BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Practice Test (For Board Examination)12videos
OSCILLATIONS
Similar Questions
Consider the following statements for a simple harmonic motion:
1. The magnitude of the velocity of the body is proportional to its displacement from the mean position.
2. The magnitude of the acceleration of the body is proportional to its displacement from the mean position.
3. The sum of the kinetic energy and potential energy of the body is always constant. Which of the statements given above is/are correct?View SolutionIf a particle is moving such that the velocity acquired is proportional to the square root of the distance covered, then its acceleration is
View Solution
Knowledge Check
- Question 1 - Select One
If a rigid body is travelling distance in proportional to the square of time, then the acceleration of this rigid body is
AconstantBIncreasingCzeroDdecreasing - Question 2 - Select One
A particle is moving on a straight line such that square of its velocity is directly proportional to distance as shown in graph. What is the acceleration of the particle ?
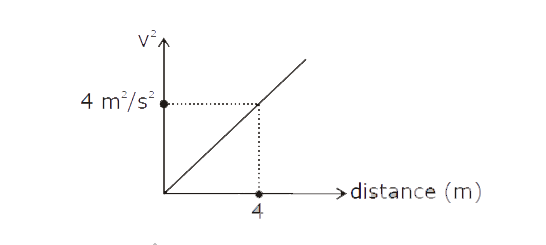 A14m/s2B1m/s2C2m/s2D12m/s2
A14m/s2B1m/s2C2m/s2D12m/s2 - Question 3 - Select One
If a point is moving in a line so that its velocity at time t is proportional to the square of the distance covered, then its acceleration at time t varies as
Acube of the distanceBthe distanceCsquare of the distanceDnone of these
The displacement of a particle is proportional to the cube of time. Then magnitude of its acceleration
View SolutionIf the displacement of a particle is proportional to the square of time, then-
View SolutionIf a particle moves such that the displacement is proportional to the square of the velocity acquired, then it acceleration is
View SolutionA particle moves in a straight line with retardation proportional to its displacement. Its loss in kinetic energy for any displacement x is proportional to
View SolutionA particle moves in a straight line with retardation proportional to its displacement. Its loss of kinetic energy for any displacement x is proportional to
View Solution

