A rabbit runs across a parking lot on which a set of coordinate axes has, strangely enough, been drawn . The coordinates (meters) of the rabbits position as functions of time t (seconds) are given by
x=−0.31t2+7.2t+28
and y=0.22t2−9.1t+30
For the rabbit in the precending sample problem , find the velocity →v at time t = 15s .
We can find →v by taking derivatives of the components of the rabbit.s position vector .
Applying the vx part of Eq. We find the x component of →v to be
vx=dxdt=ddt(−0.31t2+7.2t+28)
=−6.02t+7.2
At t = 15s , this gives vx=−2.1m/s similarly , applying the vy part of eq. we find
vy=dydt=ddt(0.22t2−9.1t+30)
=0.44−9.1
At t = 15 s , this gives vy = -2.5 m/s eqn. then yields
→v=(−2.1m/s)ˆi+(−2.5m/s)ˆj
tangent to the rabbits path and in the direction the rabbit is running at t = 15s. to get the magnitude and angle of →v either we use eq. to wire
v=√v2x+v2y=√(−2.1m/s)2+(−2.5m/s)2
=3.3m/s
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - CHECKPOINT3videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PROBLEMS50videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )3videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions57videos
OSCILLATIONS
Similar Questions
A rabbit runs across a parking lot on which a set of coordinate axes has, strangely enough, been drawn . The coordinates (meters) of the rabbits position as functions of time t (seconds) are given by
x=−0.31t2+7.2t+28
and y=0.22t2−9.1t+30
For the rabbit in the precending sample problem find the acceleration →a at time t = 15 sView SolutionA rabbit runs across a parking lot on which a set of coordinate axes has, strangely enough, been drawn . The coordinates (meters) of the rabbits position as functions of time t (seconds) are given by
x=0.31t2+7.2t+28
and y=0.22t2−9.1t+30
(a) At t =15 s , what is the rabbits position vector →r in univector notation and in magnitude - angle notation ?View Solution
Knowledge Check
- Question 1 - Select One
The coordinates of a moving particle at any time t are given by, x=2t3 and y=3t3. Acceleration of the particle is given by
A468tBt√468C234t2Dt√234 - Question 2 - Select One
Each of the four particles move along an x axis. Their coordinates (in metres) as function of time (in seconds) are given by Particle 1 : x(t) = 3.5 - 2.7t3 Particle 2 : x(t) = 3.5 + 2.7t3 Particle 3 : x(t) = 3.5 + 2.7t2 Particle 4 : x(t) = 2.5 - 3.4t - 2.7 t2 which of these particles is speeding up for t > 0?
AAll fourBOnly 1Conly 1,2, and 3Donly 2,3 and 4 - Question 3 - Select One
The coordinates of a moving particle at any time t are given by x = ct and y = bt. The speed of the particle at time t is given by
A2t(c-b)B√(c2+b2)C2t√(c2+b2)D2t√(c2+b2)
The rabbit runs enough fast to win the race.
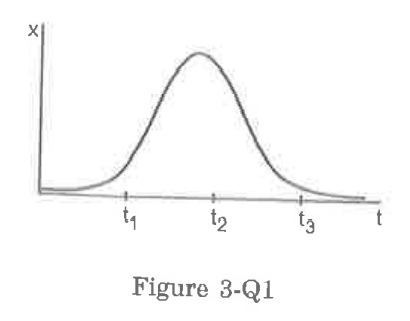
View SolutionFigure shows the x coordinate of a particle as a function of time. Find the signs of vxandaxatt=t1, t=t_2 and t=t_3.
 View Solution
View SolutionFind the locus of a point whose coordinate are given by x=t+t2,y=2t+1, where t is variable.
View SolutionThe x and y coordinates of a particle at any time t are given by x=2t+4t2andy=5t , where x and y are in metre and t in second. The acceleration of the particle at t = 5 s is
View SolutionLet the function y = f(x) be given by
x=t5−5t3−20t+7
andy=4t3−3t2−18t+3
where t∈(−2,2) then f'(x) at t = 1 isView Solution

