A rabbit runs across a parking lot on which a set of coordinate axes has, strangely enough, been drawn . The coordinates (meters) of the rabbits position as functions of time t (seconds) are given by
x=−0.31t2+7.2t+28
and y=0.22t2−9.1t+30
For the rabbit in the precending sample problem find the acceleration →a at time t = 15 s
To find the acceleration of the rabbit at time t=15 seconds, we need to follow these steps:
Step 1: Find the position functions
The position of the rabbit is given by:
- x(t)=−0.31t2+7.2t+28
- y(t)=0.22t2−9.1t+30
Step 2: Calculate the velocity functions
To find the velocity, we differentiate the position functions with respect to time t.
For the x-direction:
vx(t)=dxdt=ddt(−0.31t2+7.2t+28)=−0.62t+7.2
For the y-direction:
vy(t)=dydt=ddt(0.22t2−9.1t+30)=0.44t−9.1
Step 3: Calculate the acceleration functions
Acceleration is the derivative of velocity with respect to time.
For the x-direction:
ax(t)=dvxdt=ddt(−0.62t+7.2)=−0.62
For the y-direction:
ay(t)=dvydt=ddt(0.44t−9.1)=0.44
Step 4: Evaluate acceleration at t=15 seconds
Since the acceleration functions are constant, we can directly state:
ax=−0.62m/s2
ay=0.44m/s2
Step 5: Write the acceleration vector
The acceleration vector →a can be expressed as:
→a=ax^i+ay^j=−0.62^i+0.44^jm/s2
Step 6: Calculate the magnitude of the acceleration
To find the magnitude of the acceleration vector:
|→a|=√a2x+a2y=√(−0.62)2+(0.44)2
Calculating this gives:
|→a|=√0.3844+0.1936=√0.578≈0.76m/s2
Final Answer
The acceleration of the rabbit at t=15 seconds is:
→a=−0.62^i+0.44^jm/s2and its magnitude is 0.76m/s2.
The position of the rabbit is given by:
- x(t)=−0.31t2+7.2t+28
- y(t)=0.22t2−9.1t+30
To find the velocity, we differentiate the position functions with respect to time t.
vx(t)=dxdt=ddt(−0.31t2+7.2t+28)=−0.62t+7.2
vy(t)=dydt=ddt(0.22t2−9.1t+30)=0.44t−9.1
Acceleration is the derivative of velocity with respect to time.
ax(t)=dvxdt=ddt(−0.62t+7.2)=−0.62
ay(t)=dvydt=ddt(0.44t−9.1)=0.44
Since the acceleration functions are constant, we can directly state:
ax=−0.62m/s2
ay=0.44m/s2
The acceleration vector →a can be expressed as:
→a=ax^i+ay^j=−0.62^i+0.44^jm/s2
To find the magnitude of the acceleration vector:
|→a|=√a2x+a2y=√(−0.62)2+(0.44)2
Calculating this gives:
|→a|=√0.3844+0.1936=√0.578≈0.76m/s2
The acceleration of the rabbit at t=15 seconds is:
→a=−0.62^i+0.44^jm/s2and its magnitude is 0.76m/s2.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - CHECKPOINT3videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PROBLEMS50videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )3videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions57videos
OSCILLATIONS
Similar Questions
A rabbit runs across a parking lot on which a set of coordinate axes has, strangely enough, been drawn . The coordinates (meters) of the rabbits position as functions of time t (seconds) are given by
x=−0.31t2+7.2t+28
and y=0.22t2−9.1t+30
For the rabbit in the precending sample problem , find the velocity →v at time t = 15s .View SolutionA rabbit runs across a parking lot on which a set of coordinate axes has, strangely enough, been drawn . The coordinates (meters) of the rabbits position as functions of time t (seconds) are given by
x=0.31t2+7.2t+28
and y=0.22t2−9.1t+30
(a) At t =15 s , what is the rabbits position vector →r in univector notation and in magnitude - angle notation ?View Solution
Knowledge Check
- Question 1 - Select One
Each of four particles moves along an x axis. Their coordinates (in meters) as function of time (in seconds) are given by
Particle 1:x(t)=3.5−2.7t3
Particle :2 x(t)=3.5+2.7t3
particle 3: x(t)=3.5+2.7t2
particle 4: x(t)=3.5−3.4t−2.7t2
Which of these particles have constant acceleration ?AAll fourBonly 1 and 2Conly 2 and 3Donly 3 and 4 - Question 2 - Select One
The coordinates of a moving particle at any time t are given by, x=2t3 and y=3t3. Acceleration of the particle is given by
A468tBt√468C234t2Dt√234 - Question 3 - Select One
Each of the four particles move along an x axis. Their coordinates (in metres) as function of time (in seconds) are given by Particle 1 : x(t) = 3.5 - 2.7t3 Particle 2 : x(t) = 3.5 + 2.7t3 Particle 3 : x(t) = 3.5 + 2.7t2 Particle 4 : x(t) = 2.5 - 3.4t - 2.7 t2 which of these particles is speeding up for t > 0?
AAll fourBOnly 1Conly 1,2, and 3Donly 2,3 and 4
The rabbit runs enough fast to win the race.
View SolutionFigure shows the x coordinate of a particle as a function of time. Find the signs of vxandaxatt=t1, t=t_2 and t=t_3.
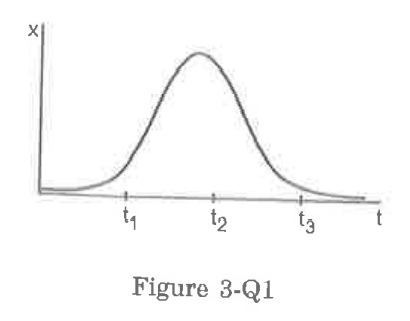 View Solution
View SolutionA rabbit runs across a parking lot. The path is such that components of rabbit's position with respect to an origin of co-ordinates as function of time are x = R + 10 and y -9t + 5. Here x, y are in meter and t in second. The magnitude of rabbit's displacement during first 5 seconds is
View SolutionThe coordinates of a moving particle at any time t are given by x = ct and y = bt. The speed of the particle at time t is given by
View SolutionA particle's position as a function of time is described as y(t)=2t2+3t+4. What is the average velocity of the particle from t=0 to t=3 sec ?
View Solution

