A volleyball is spiked so that it has an initial velocity of 15 m/s directed downward at an angle of 55∘ below the horizontal. What is the horizontal component of the ball's velocity when the opposing player fields the ball?
6.8 m/s
8.6 m/s
12 m/s
18 m/s
The correct Answer is:B
To solve the problem, we need to find the horizontal component of the volleyball's initial velocity when it is spiked. The volleyball is given an initial velocity of 15 m/s directed downward at an angle of 55 degrees below the horizontal.
1. Identify the Given Information:
- Initial velocity v=15m/s
- Angle θ=55∘ (below the horizontal)
2. Understand the Components of Velocity:
- The initial velocity can be broken down into two components: horizontal and vertical.
- The horizontal component vx can be calculated using the cosine of the angle, since it is adjacent to the angle.
3. Calculate the Horizontal Component:
vx=v⋅cos(θ)
Substituting the values:
vx=15m/s⋅cos(55∘)
4. Calculate cos(55∘):
- Using a calculator, we find:
cos(55∘)≈0.5736
5. Substitute Back to Find vx:
vx=15m/s⋅0.5736≈8.604m/s
6. Round the Result:
- Rounding to one decimal place, we get:
vx≈8.6m/s
Final Answer:
The horizontal component of the ball's velocity when the opposing player fields the ball is approximately 8.6 m/s.
---
- Initial velocity v=15m/s
- Angle θ=55∘ (below the horizontal)
- The initial velocity can be broken down into two components: horizontal and vertical.
- The horizontal component vx can be calculated using the cosine of the angle, since it is adjacent to the angle.
vx=v⋅cos(θ)
Substituting the values:
vx=15m/s⋅cos(55∘)
- Using a calculator, we find:
cos(55∘)≈0.5736
vx=15m/s⋅0.5736≈8.604m/s
- Rounding to one decimal place, we get:
vx≈8.6m/s
The horizontal component of the ball's velocity when the opposing player fields the ball is approximately 8.6 m/s.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)3videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (LINKED COMPREHENSION)14videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PROBLEMS50videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )3videos
MOTION ALONG A STRAIGHT LINE
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions57videos
OSCILLATIONS
Similar Questions
A body is projected horizontally from the top of a tower with initial velocity 18ms−1. It hits the ground at angle 45∘. What is the vertical component of velocity when it strikes the ground ?
View SolutionA ball is kicked at an angle of 30∘ with the vertical. If the horizontal component of its velocity is 19.6ms−1, find the maximum height and horizontal range.
View Solution
Knowledge Check
- Question 1 - Select One
The velocity of a body is 20 m/s making an angle of 30∘ with the horizontal, the vertical component of velocity is
A20m/sB17.32m/sC10m/sD7m/s - Question 2 - Select One
Assume that a ball is kicked at an angle of 60∘ with the horizontal, so if the horizontal component of its velocity is 19.6ms−1, determine its maximum height.
A58.8mB40mC120mD60m - Question 3 - Select One
A particle is projected with a velocity of 25m/s at an angle of 30∘ with the horizontal . Calculate
(i) The maximum height ,
(ii) time of flight and
(iii) horizontal range .A562 mB286 mC188 mD1130 m
A ball is projected from the floor of a long hall having a roof height of H=10m. The ball is projected with a velocity of u=25ms–1 making an angle of θ=37∘ to the horizontal. On hitting the roof the ball loses its entire vertical component of velocity but there is no change in the horizontal component of its velocity. The ball was projected from point A and its hits the floor at B. Find distance AB.
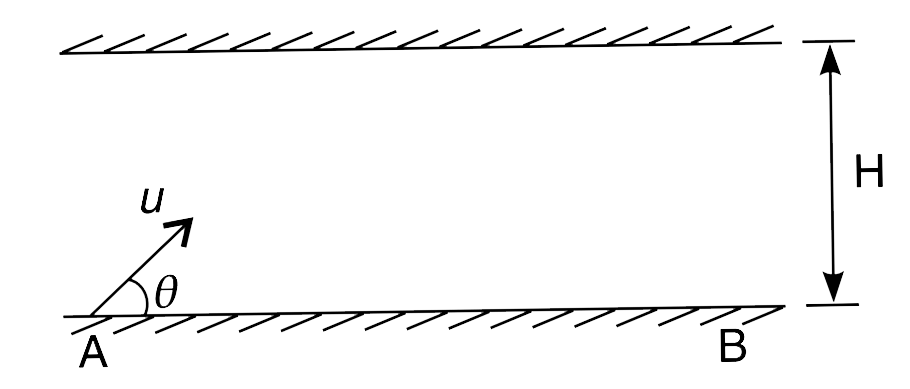 View Solution
View SolutionA body projected at an angle with the horizontal has a range 300 m. the time of flight is 6s, then the horizontal component of velocity is
View SolutionA ball is projected horizontal from the top of a tower with a velocity v0. It will be moving at an angle of 60∘ with the horizontal after time.
View SolutionA particle is projected with velocity of 10ms at an angle of 15° with horizontal.The horizontal range will be(g=10ms2)
View SolutionA ball is projected from the ground at angle θ with the horizontal. After 1s, it is moving at angle 45∘ with the horizontal and after 2s it is moving horizontally. What is the velocity of projection of the ball ?
View Solution

