A car drives straight off the edge of a cliff that is 54 m high. The police at the scene of the accident observe that the point of impact is 130 m from the base of the cliff. How fast was the car traveling when it went over the cliff?
39 m/s
53 m/s
22 m/s
45 m/s
The correct Answer is:A
To solve the problem of how fast the car was traveling when it went over the cliff, we can break it down into a few steps.
1. Identify the Given Information:
- Height of the cliff (h) = 54 m
- Horizontal distance from the base of the cliff to the point of impact (d) = 130 m
- Acceleration due to gravity (g) = 9.8 m/s²
2. Calculate the Time of Fall:
The vertical motion can be analyzed using the second equation of motion:
h=12gt2
Rearranging for time (t):
t2=2hg
Substituting the values:
t2=2×549.8
t2=1089.8≈11.02
Taking the square root:
t≈√11.02≈3.32 seconds
3. Calculate the Horizontal Velocity:
Since there is no horizontal acceleration, the horizontal velocity (u) remains constant. We can find it using the formula:
u=dt
Substituting the known values:
u=1303.32≈39.24 m/s
4. Final Result:
The speed of the car when it went over the cliff is approximately 39.24 m/s.
- Height of the cliff (h) = 54 m
- Horizontal distance from the base of the cliff to the point of impact (d) = 130 m
- Acceleration due to gravity (g) = 9.8 m/s²
The vertical motion can be analyzed using the second equation of motion:
h=12gt2
Rearranging for time (t):
t2=2hg
Substituting the values:
t2=2×549.8
t2=1089.8≈11.02
Taking the square root:
t≈√11.02≈3.32 seconds
Since there is no horizontal acceleration, the horizontal velocity (u) remains constant. We can find it using the formula:
u=dt
Substituting the known values:
u=1303.32≈39.24 m/s
The speed of the car when it went over the cliff is approximately 39.24 m/s.
Topper's Solved these Questions
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
3 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (LINKED COMPREHENSION)
14 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PROBLEMS
50 Videos
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )
3 Videos
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions
57 Videos
Similar Questions
Aman on deck of a ship is 12 m above the water level. He observes that the angle of the elevation of the top of a cliff is 45∘ and the angle of depression of its base is 30∘. Calculate the distance of the cliff from the ship and the height of the cliff.
View SolutionA man on the deck of a ship is 10m above the water level. He observes that the angle of elevation of the top of a cliff is 45o and the angle of depression of the base is 30o . Calculate the distance of the cliff from the ship and the height of the cliff.
View Solution
Knowledge Check
A pellet gun is fired straight downward from the edge of a cliff that is 15 m above the ground. The pallet strickes the ground with a speed of 27 m/s. How far above the cliff edge would the pellet have gone had the gun been fired straight upward ?
A4.5 mB22 mC15 mD29 mFrom the top of a cliff 50 m high, the angles of depression of the top and bottom of a tower are observed to be 30∘ and 45∘. The height of tower is
A50mB50√3mC50(√3−1)mD50(1−√33)mFrom the top of a cliff 50m high, the angles of depression of the top and bottom of a tower are observed to be 30∘ and 45∘ The height of tower is
A50 mB50√3C50(√3−1)D50(1−√33)m
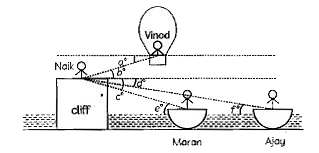
Mr. Naik is a paramilitary Intelligence Corps officer who is tasked with planning a coup on the enemy at a certain date. Currently he is inspecting the area standing on top of the cliff. Agent Vinod is on a hot air ballon in the sky. When Mr. Naik looks down below the cliff towards the sea, he has Ajay and Maran in boats positioned to get a good vantage point.
The main goal is to scope out the range and angles at which they should train their soldiers.
Ajay's boat is 25 m away from the base of the cliff. If <d=30∘. What is the height of the cliff? (use √3=1.73)
View SolutionA small ball rolls horizontally off the edge of a tabletop that is 1.50 m high. It strikes the floor at a point 1.52 m horizontally from the table edge. (a) How long is the ball in the air? (b) What is its speed at the instant it leaves the table?
View SolutionA man on the deck of a ship 12 m above water level, observes that the angle of elevation of the top of a cliff is 60∘ and the angle of depression of the base of the is 30∘. Find the distance of the cliff from the ship and the height of the cliff. [use √3=1.732)
View SolutionA man fires a shot and hears an echo from a cliff after 2s. He walks 85m towards the cliff and the echo of a second shot is now heard after 1.4s. What is the velocity of sound and how far was the man from the cliff when he first heard the echo ?
View SolutionFrom the top of a cliff 50m high, the angles of depression of the top and bottom of a tower are observed to be 30∘ and 45∘ The height of tower is
View Solution
