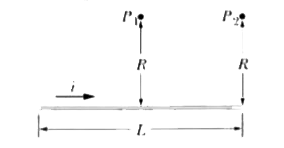
In Fig 29−40 point P2 is at perpendicular distance R=25.1 cm from one end of a straight wire of length L=13.6 cm carrying current i=0.500 A. (Note that the wire is not long ) (a) What is the magnitude of the magnetic field at P2 ? (b) If the point of measurement is moved from P2 to P1 does the field magnitude increase, decrease, or remain the same ?
The correct Answer is:94.9 nT; (b) increase
To solve the problem, we will use the formula for the magnetic field B at a point due to a finite straight wire carrying current. The formula is given by:
B=μ0I4πr(sinα+sinβ)
where:
- μ0 is the permeability of free space (4π×10−7T m/A),
- I is the current in the wire,
- r is the perpendicular distance from the wire to the point of interest,
- α is the angle subtended by the wire at the point of interest,
- β is the angle subtended by the wire at the other end (which is zero in this case).
1. Identify Given Values:
- Length of the wire, L=13.6cm=0.136m
- Current, I=0.500A
- Perpendicular distance, R=25.1cm=0.251m
2. Calculate Angles:
- The angle α can be found using the tangent function:
tanα=LR=0.1360.251
- Calculate α:
α=tan−1(0.1360.251)
3. Calculate sinα:
- Using the right triangle formed, we can find sinα:
sinα=L√L2+R2=0.136√(0.136)2+(0.251)2
4. Substitute Values into the Magnetic Field Formula:
- Since β=0, sinβ=0:
B=μ0I4πR(sinα+0)
- Substitute μ0=4π×10−7T m/A, I=0.500A, and R=0.251m:
B=(4π×10−7)×0.5004π×0.251sinα
5. Calculate the Magnetic Field B:
- After calculating sinα and substituting it back into the equation, compute B:
B≈94.9×10−9T=94.9nT
Part (b): Change in Magnetic Field Magnitude
- If the point of measurement is moved from P2 to P1, which is closer to the wire, the magnetic field magnitude will increase. This is because the magnetic field strength is inversely proportional to the distance from the wire.
- μ0 is the permeability of free space (4π×10−7T m/A),
- I is the current in the wire,
- r is the perpendicular distance from the wire to the point of interest,
- α is the angle subtended by the wire at the point of interest,
- β is the angle subtended by the wire at the other end (which is zero in this case).
- Length of the wire, L=13.6cm=0.136m
- Current, I=0.500A
- Perpendicular distance, R=25.1cm=0.251m
- The angle α can be found using the tangent function:
tanα=LR=0.1360.251
- Calculate α:
α=tan−1(0.1360.251)
- Using the right triangle formed, we can find sinα:
sinα=L√L2+R2=0.136√(0.136)2+(0.251)2
- Since β=0, sinβ=0:
B=μ0I4πR(sinα+0)
- Substitute μ0=4π×10−7T m/A, I=0.500A, and R=0.251m:
B=(4π×10−7)×0.5004π×0.251sinα
- After calculating sinα and substituting it back into the equation, compute B:
B≈94.9×10−9T=94.9nT
- If the point of measurement is moved from P2 to P1, which is closer to the wire, the magnetic field magnitude will increase. This is because the magnetic field strength is inversely proportional to the distance from the wire.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Single Correct)36videos
MAGNETIC FIELDS DUE TO CURRENTS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (More Than one correct choice )12videos
MAGNETIC FIELDS DUE TO CURRENTS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Check point4videos
MAGNETIC FIELDS DUE TO CURRENTS
- BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (Integer Type)6videos
INTERFERENCE AND DIFFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Practice Questions (Integer type )7videos
MAGNETIC FORCE
Similar Questions
In Fig. 29−40 point P, is at distance R=24.0 cm on the perpendicular bisector of a straight wire of length L=18.0cm carrying current i=58.2 mA. (Note that the wire is not long). What are the (a) magnitude and (b) direction of the magnetic field at P, due to i ? (c ) If R is increased, what happens to the magnitude of the field ?
 View Solution
View SolutionA long straight wire carries a current of 35 A. What is the magnitude of the field →B at a point 20 cm from the wire?
View Solution
Knowledge Check
- Question 1 - Select One
The magnetic field at a perpendicular distance of 2 cm from an infinite straight current carrying conductor is 2×10−6 T. The current in the wire is
A0.1AB0.2AC0.4AD0.8A - Question 2 - Select One
The magnetic field at a perpendicular distance of 2cm from an infinite straight current carrying conductor is 2×10−6T. The current in the wire is
A0⋅1AB0⋅2AC0⋅4AD0⋅8A - Question 3 - Select One
Figure shows a straight wire of length l carrying a current i. Find the magnitude of magnetic field produced by the current at point P.
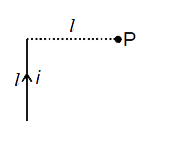 A√2μ0i3π1B√2μ0i8π1Cμ0i2π1D√2μ0iπl
A√2μ0i3π1B√2μ0i8π1Cμ0i2π1D√2μ0iπl
A long straight wire carries a current of 35 A. What is the magnitude of the field →B at a point 20 cm from the wire?
View SolutionCalculate the magnitude of the magnetic field at point P as shown in Fig, in terms of R,I1andI2.
 View Solution
View SolutionA conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be
 View Solution
View SolutionCalculate the value of magnetic field at a distance of 2 cm from a very long straight wire carrying a current 5 A
View SolutionA straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the fig. Find the magnitude and direction of the magnetic field at the centre of the arc.
 View Solution
View Solution

