An electron is moving with a speed of m//s when it encounters a magnetic field of T. The direction of the magnetic field makes an angle of with respect to the velocity of the electron. What is the magnitude of the magnetic force on the electron ?
N
N
N
N
The correct Answer is:B
To find the magnitude of the magnetic force acting on the electron, we can use the formula for the magnetic force on a charged particle moving in a magnetic field:
F=q⋅v⋅B⋅sin(θ)
Where:
- F is the magnetic force,
- q is the charge of the electron,
- v is the velocity of the electron,
- B is the magnetic field strength,
- θ is the angle between the velocity and the magnetic field.
Step 1: Identify the known values
- Charge of the electron, q=1.6×10−19C
- Velocity of the electron, v=3.5×105m/s
- Magnetic field strength, B=0.6T
- Angle, θ=60∘
Step 2: Calculate sin(θ)
We need to find sin(60∘):
sin(60∘)=√32
Step 3: Substitute the values into the formula
Now we can substitute the known values into the magnetic force formula:
F=(1.6×10−19C)⋅(3.5×105m/s)⋅(0.6T)⋅(√32)
Step 4: Calculate the force
First, calculate the product of the constants:
1. Calculate 1.6×10−19⋅3.5×105:
1.6×3.5=5.6
5.6×10−14C m/s
2. Now multiply by 0.6:
5.6×0.6=3.36
3.36×10−14C m/s
3. Finally, multiply by √32:
√32≈0.866
3.36×0.866≈2.91
2.91×10−14N
Final Result
Thus, the magnitude of the magnetic force on the electron is approximately:
F≈2.9×10−14N
- F is the magnetic force,
- q is the charge of the electron,
- v is the velocity of the electron,
- B is the magnetic field strength,
- θ is the angle between the velocity and the magnetic field.
- Charge of the electron, q=1.6×10−19C
- Velocity of the electron, v=3.5×105m/s
- Magnetic field strength, B=0.6T
- Angle, θ=60∘
We need to find sin(60∘):
sin(60∘)=√32
Now we can substitute the known values into the magnetic force formula:
F=(1.6×10−19C)⋅(3.5×105m/s)⋅(0.6T)⋅(√32)
First, calculate the product of the constants:
1. Calculate 1.6×10−19⋅3.5×105:
1.6×3.5=5.6
5.6×10−14C m/s
5.6×0.6=3.36
3.36×10−14C m/s
√32≈0.866
3.36×0.866≈2.91
2.91×10−14N
Thus, the magnitude of the magnetic force on the electron is approximately:
F≈2.9×10−14N
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (More Than one correct choice )12videos
MAGNETIC FIELDS DUE TO CURRENTS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Linked Comprehension)16videos
MAGNETIC FIELDS DUE TO CURRENTS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Problems45videos
MAGNETIC FIELDS DUE TO CURRENTS
- BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (Integer Type)6videos
INTERFERENCE AND DIFFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Practice Questions (Integer type )7videos
MAGNETIC FORCE
Similar Questions
He2+ ion travels at right angles to a magnetic field of 0.80T with a velocity of 105ms. Find the magnitude of the magnetic force on the ion.
View SolutionAn electron is moving with a velocity of 5×107 m/s in a magnetic field of 6×10−4 T perpendicular to it. What is the frequency? Also find the energy of electron in MeV.
View Solution
Knowledge Check
- Question 1 - Select One
An electron entres a magnetic field whose direction is perpendicualr to the velocity of the electron. Then
AThe speed of the electron will increaseBThe speed of the electron will decreaseCThe speed of the electron will remain the same.DThe velocity fo the electron will remain the same. - Question 2 - Select One
An electron having momentum 2.4×10−23 kg m s−1 enters a region of uniform magnetic field of 0.15 T. The field vector makes an angle of 30∘ with the initial velocity vector of the electron. The radius of the helical path of the electron in the field shall be
A2mmB1mmC√32 mmD0.5mm - Question 3 - Select One
A proton moving with a velocity of 2.5×107ms, enter a magnetic feildof 2T, making an angle of 30◦ with the magnetic field. The force acting on the proton
A2×10−12NB3×10−12NC4×10−12ND6×10−12N
An electron (charge q coulomb) enters a magnetic field of Hweber/m2 with a velocity of vm/s in the same direction as that of the field the force on the electron is
View SolutionAn electron having momentum 2.4×10−23 kg m"/"s enters a region of unifom magnetic field of 0.15 T. The field vector makes an angle of 30∘ with the initial velocity Vector of the electron. The radius of the helical path of the electron in the field shall be
View SolutionTwo electrons are moving with speed of 5×105 m/s parallel to each other, then the electrostatic and magnetic force between them is
View SolutionAn electron enters a region that contains a magnetic field directed into the page as shown. The velocity vector of the electron makes an angle of 30∘ with the +y axis. What is the direction of the magnetic force on the electron when it enters the field ?
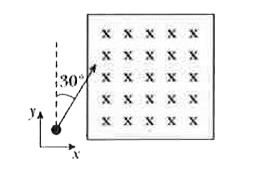 View Solution
View SolutionA proton moving withh a velocity 2.5×107m/s enters a magnetic field of intensity 2.5T making an angle 30∘ with the magnetic field. The force on the proton is
View Solution

