Two electrons are moving with speed of 5×105 m/s parallel to each other, then the electrostatic and magnetic force between them is
5×105
2.5×104
3.6×105
4.4×103
The correct Answer is:D
To solve the problem of finding the electrostatic and magnetic forces between two electrons moving parallel to each other with a speed of 5×105 m/s, we will follow these steps:
Step 1: Understand the Forces Involved
We need to consider both the electrostatic force and the magnetic force between the two electrons.
Step 2: Calculate the Electrostatic Force
The electrostatic force Fe between two charges is given by Coulomb's law:
Fe=k⋅|q1⋅q2|r2
where:
- k is Coulomb's constant, approximately 9×109N m2/C2,
- q1 and q2 are the charges of the electrons, which is the elementary charge e≈1.6×10−19C,
- r is the distance between the two electrons.
Substituting the values:
Fe=9×109⋅(1.6×10−19)2r2
Step 3: Calculate the Magnetic Force
The magnetic force Fm on a charge moving in a magnetic field is given by:
Fm=q⋅v⋅B
where:
- B is the magnetic field created by one of the moving electrons at the location of the other,
- v is the speed of the electrons.
To find B, we use the formula for the magnetic field due to a moving charge:
B=μ04π⋅q⋅vr2
where μ0 is the permeability of free space, approximately 4π×10−7T m/A.
Substituting B into the magnetic force equation:
Fm=q⋅v⋅(μ04π⋅q⋅vr2)
Fm=μ0⋅q2⋅v24πr2
Step 4: Find the Ratio of Electrostatic to Magnetic Force
Now we find the ratio FeFm:
FeFm=k⋅q2r2μ0⋅q2⋅v24πr2=k⋅4πμ0⋅v2
Step 5: Substitute Known Values
Substituting k=9×109, μ0=4π×10−7, and v=5×105:
FeFm=9×109⋅4π4π×10−7⋅(5×105)2
=9×10910−7⋅25×1010=9×10925×103=925×106
Step 6: Final Calculation
Calculating this gives:
FeFm=0.36×106=3.6×105
Conclusion
Thus, the ratio of the electrostatic force to the magnetic force between the two electrons is 3.6×105.
---
We need to consider both the electrostatic force and the magnetic force between the two electrons.
The electrostatic force Fe between two charges is given by Coulomb's law:
Fe=k⋅|q1⋅q2|r2
where:
- k is Coulomb's constant, approximately 9×109N m2/C2,
- q1 and q2 are the charges of the electrons, which is the elementary charge e≈1.6×10−19C,
- r is the distance between the two electrons.
Fe=9×109⋅(1.6×10−19)2r2
The magnetic force Fm on a charge moving in a magnetic field is given by:
Fm=q⋅v⋅B
where:
- B is the magnetic field created by one of the moving electrons at the location of the other,
- v is the speed of the electrons.
B=μ04π⋅q⋅vr2
where μ0 is the permeability of free space, approximately 4π×10−7T m/A.
Fm=q⋅v⋅(μ04π⋅q⋅vr2)
Fm=μ0⋅q2⋅v24πr2
Now we find the ratio FeFm:
FeFm=k⋅q2r2μ0⋅q2⋅v24πr2=k⋅4πμ0⋅v2
Substituting k=9×109, μ0=4π×10−7, and v=5×105:
FeFm=9×109⋅4π4π×10−7⋅(5×105)2
=9×10910−7⋅25×1010=9×10925×103=925×106
Calculating this gives:
FeFm=0.36×106=3.6×105
Thus, the ratio of the electrostatic force to the magnetic force between the two electrons is 3.6×105.
Topper's Solved these Questions
Similar Questions
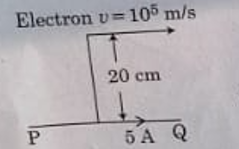
An infinitely long straight consuctor carries a current of 5A as shown. An electron is moving with a speed of 105ms parallel to the conductor. The perpendicular distance between the electron and the conductor is 20cm at an instant. Calculate the magnitude of the force experienced by the electron at that instant.
 View Solution
View SolutionThe distance between the electron and proton in hydrogen atom is 5.3×10−11 m. Determine the magnitude of the ratio of electrostatic and gravitational force between them. Given me=9.1×10−31 kg, mp=1.67×10−27 kg, e=1.6×10−19C and G=6.67×10−11Nm2kg2.
View Solution
Knowledge Check
- Question 1 - Select One
If two protons are moving with speed v=4.5×105m/s parallel to each other then find the ratio of electrostatic and magnetic force between them : -
A4.4×105B2.2×105C3.3×105D1.1×105 - Question 2 - Select One
Two electrons move parallel to each other with equal speed 'V' the ratio of magnetic & electric force between them is
AV/CBC/VCV2/C2DC2/V2 - Question 3 - Select One
Two streams of electrons are moving parallel to each other in the same direction. They
Aattract each otherBrepel each otherCcancel the electric field of each otherDcancel the magnetic field of each other
Two electrons move parallel to each other with equal speed 'V' the ratio of magnetic & electric force between them is
View SolutionAn electron is moving with a speed of 3.5×105 m//s when it encounters a magnetic field of 0.60 T. The direction of the magnetic field makes an angle of 60.0∘ with respect to the velocity of the electron. What is the magnitude of the magnetic force on the electron ?
View SolutionTwo protons are a distance of 1×10−10cm from each other. The force acting on them are
View SolutionA long wire carries a current of 5A. An electron at a distance of 50 cm from this wire is moving with a speed of 107 m/s What is the force acting on the electron, when it moves directly towards the wire ?
View SolutionTwo protons parallel to each other, keeping distane r between them, both moving with same velocity →V Then the ratio of the electric is magnetic force of interaction between them is .
View Solution

