Apparent velocity of fish floating in tank
A tank is filled with water up to a height of 15cm and a fish is floating inside at a depth of 10cm. The tank is now being drained so that the surface moves down with a velocity of 1cm/s. An observer is viewing the fish from a height of 10cm.
(a) Find the apparent velocity of the fish as seen by the observer.
Find the apparent velocity of the observer as seen by the fish.
If the object moves with a velocity v inside the medium, its apparent velocity can be found by rate of change of apparent depth.
Let us assume that xm= depth of x with respect to surface. Then
dappnrefracted=dactualnincident
Here, the depth of image is changing because the depth of the object is changing with respect to surface.
Differentiating both sides, we get
VISnr=VOSni⇒VI−VSnr=VO−VSni
where VIS is the velocity of image with respect to the surface and VOS is the object of image with respect to the surface. These refer to the velocities in the normal direction .In a direction parallel to the surface, the velocity of the image will be the same as the velocity of the object. Calculation : Assuming downward direction to be positive, the velocity of the object (fish) is zero (fish is floating). Now VS=+1cm/s. Therefore,
VISnr=VOSni
VIS=nrniVOS=143×(VO−VS)−34m/s
VIS=VI−VS
−34+1=VI⇒VI=14m/s (34-5)
Again
VIS43=VOS1=VS×43=−43m/s
VI−VS=43
VI=1−−43=−13cm/s
Learn : The fish seems to be at a lesser depth than it actually is. So when depth of water decreases, the image of fish will approach its actual position. So, VI should be downward in Eq. 34-5. A similar argument can be applied to Eq. 34-6
Topper's Solved these Questions
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Check point
6 Videos
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Problems
44 Videos
- GEOMETRICAL OPTICS : REFLECTION BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
4 Videos
Similar Questions
Find out the following in the figure shown below :
(a) The apparent speed of the fish as observed by the bird
(b) The apparent speed of the bird as observed by the fish
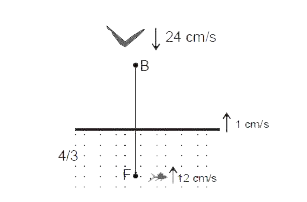
View SolutionA fish is 60 cm under water (μ=4/3). A bird directly overhead looks at the fish. If the bird is at a distance of 120 cm from the water surface, (a) What is the apparent position of the fish as seen by the bird and (b) what is the apparent position of the bird as seen by the fish?
View Solution
Knowledge Check
A fish which is at a depth of 12 cm in water (μ=43) is viewed by an observer on the bank of a lake. Its apparent depth as observed by the observer is :
A3 cmB9 cmC12 cmD16 cmA fish at a depth of 12cm in water is viewed by an observer on the bank of a lake. To what height the images of the fish is raised ?
A9cmB12cmC3.8cmD3cmA tank is filled with water to a height of 15.5cm. The apparent depth of a needle lying at the bottom of the tank is measured by a microscope to be 8.5cm. If water is replaced by a liquid of refractive index 1.94 up to the same height by what distance would the microscope have to be moved to focus on the needle again ?
A1.00cmB2.37cmC0.51cmD3.93cm
Suppose now that the fish sees the boy. Find (a) apparent distance of eye as seen by fish. (b) apparent distance of image of eye as seen by fish.
View SolutionFind out the following in the figure shown below :

(a) The apparent distance of the fish from the surface as observed by the bird
(b) The apparent distance of the bird from the surface as observed by the fish
View SolutionThe apparent depth of an object at the bottom of tank filled with a liquid of refractive index 1.3 is 7.7 cm. what is the actual depth of the liquid in the tank ?
View SolutionA pond of depth 20 cm is filled with water of refractive index 4/3. Calculate apparent depth of the tank when viewed normally.
View SolutionA plane mirror is fixed at the bottom of a vessel as shown in the figure. Water of refractive index μ is filled up to a height h in the vessel. There is a fish at a height h/2 from bottom of vessel and there is a bird at a height h above the surface of water in the vessel.
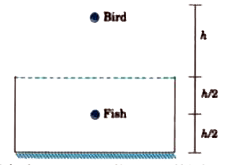
(a) Calculate apparent distance of bird as seen by the fish.
(b) Calculate apparent distance of image of bird in mirror as seen by the fish.
(c) Calculate apparent distance of fish as seen by the bird.
(d) Calculate apparent distance of image of fish in the mirror as seen by the bird.
View Solution
