A section of a spherical shell of outer radius R0 and inner radius R1 is cut, and used as a lens. The light first strikes what was originally the outer surface of the glass shell. Which of the following statements about the resulting lens is true ?
The lens is converging
The lens is diverging
The lens has zero focal length
The lens has infinite focal length
The correct Answer is:B
To solve the problem regarding the lens formed by a section of a spherical shell with outer radius R0 and inner radius R1, we can follow these steps:
Step 1: Understand the Geometry of the Lens
The lens is formed by cutting a section of a spherical shell. The outer surface of the shell has a radius R0 and the inner surface has a radius R1. When light strikes the outer surface first, it will refract according to the lens maker's formula.
Hint: Visualize the lens by sketching the spherical shell and marking the outer and inner radii.
Step 2: Apply the Lens Maker's Formula
The lens maker's formula is given by:
1F=(n−1)(1R1−1R2)
where n is the refractive index of the lens material, R1 is the radius of curvature of the first surface (outer surface), and R2 is the radius of curvature of the second surface (inner surface).
Hint: Identify which radius corresponds to which surface based on the direction of light travel.
Step 3: Determine the Sign of the Radii
For the outer surface (where light first strikes), the radius R1 is positive because it is convex. For the inner surface, R2 is negative because it is concave when viewed from the direction of incoming light.
Hint: Remember the sign convention: radii are positive for convex surfaces and negative for concave surfaces when following the direction of light.
Step 4: Substitute the Values into the Formula
Using the sign convention:
- R1=R0 (positive)
- R2=−R1 (negative)
Substituting these values into the lens maker's formula gives:
1F=(n−1)(1R0−(−1R1))=(n−1)(1R0+1R1)
Hint: Ensure you keep track of the signs while substituting values into the formula.
Step 5: Analyze the Resulting Lens Type
Since both terms 1R0 and 1R1 are positive, the overall result of 1F will also be positive. This indicates that the lens is converging.
Hint: A positive focal length indicates a converging lens, while a negative focal length indicates a diverging lens.
Conclusion
The resulting lens formed by the section of the spherical shell is a converging lens.
Final Statement: The correct statement about the resulting lens is that it acts as a converging lens.
The lens is formed by cutting a section of a spherical shell. The outer surface of the shell has a radius R0 and the inner surface has a radius R1. When light strikes the outer surface first, it will refract according to the lens maker's formula.
The lens maker's formula is given by:
1F=(n−1)(1R1−1R2)
where n is the refractive index of the lens material, R1 is the radius of curvature of the first surface (outer surface), and R2 is the radius of curvature of the second surface (inner surface).
For the outer surface (where light first strikes), the radius R1 is positive because it is convex. For the inner surface, R2 is negative because it is concave when viewed from the direction of incoming light.
Using the sign convention:
- R1=R0 (positive)
- R2=−R1 (negative)
1F=(n−1)(1R0−(−1R1))=(n−1)(1R0+1R1)
Since both terms 1R0 and 1R1 are positive, the overall result of 1F will also be positive. This indicates that the lens is converging.
The resulting lens formed by the section of the spherical shell is a converging lens.
Topper's Solved these Questions
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Practice questions(More than one correct choice type)
14 Videos
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Practice questions(Linked Comprehension)
2 Videos
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Problems
44 Videos
- GEOMETRICAL OPTICS : REFLECTION BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
4 Videos
Similar Questions
A metallic spherical shell has an inner radius R1 and outer radius R2. A charge is placed at the centre of the spherical cavity. The surface charge density on the inner surface is

View SolutionFigure shows a cross-section ofa spherical metal shell of inner radius R and out radius ZR. A point charge q is ·located at a distanceR/2 from the centre of the shell. If the shell is electrically neutral, then which of the following statements is/are correct :
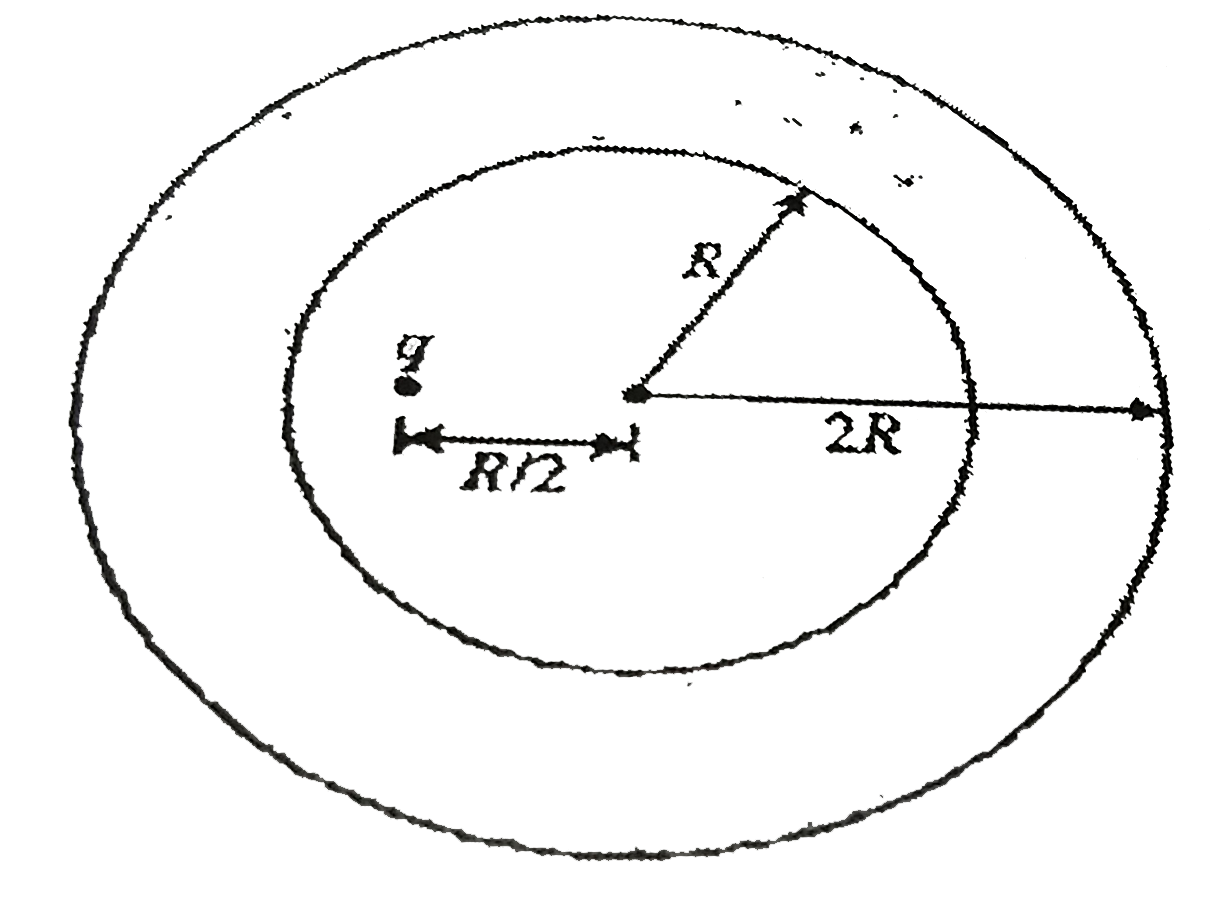
View Solution
Knowledge Check
A charge +q is placed somewhere inside the cavity of a thick conducting spherical shell of inner radius R1 and outer radius R2. A charge – Q is placed at a distance r>R2 from the centre of the shell. Then the electric field in the hollow cavity-
Adepends on both +q and – QBis zeroCis only that due to -QDis only that due to +q
A point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View SolutionA conducting spherical shell having inner radius a and outer radius b carries a net charge Q. If a point charge q is placed at the centre of this shell, then the surface charge density on the outer surface of the shell is given as:
View SolutionA spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q:
(a) A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell?
(b) Is the electric field inside a cavity (with no charge) zero even if the shell is not spherical, but has any irregular shape? Explain.
View SolutionA spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
(a) A charge q is placed at the center of the shell. What is the surface charge density on the inner and outer surfaces of the shell ?
(b) Is the electric field intensity inside a cavity (with no charge) zero, even if the shell is not spherical, but has any irregular shape ? Explain.
View SolutionA spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
(a) A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell ?
View SolutionA metal spherical shell has an inner radius R1 and outer radius R2. A charge Q is placed at the center of the spherical cavity. What will be surface charge density on (i) the inner surface, and (ii) the outer surface ?
View SolutionHeat flows radially outwards through a spherical shell of outside radius R2 and inner radius R1. The temperature of inner surface of shell is θ1 and that of outer is θ2. At what radial distance from centre of shell the temperature is just half way between θ1andθ2?
View Solution
