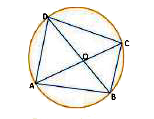
A cyclic quadrailatral ABCD is such that AB=BC, AD=Dc AC⊥BD,∠CAD=θ Then the angle ∠ABC
θ
θ2
2θ
3θ
The correct Answer is:c
To solve the problem, we need to find the angle ∠ABC in the cyclic quadrilateral ABCD with the given conditions. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the properties of the cyclic quadrilateral
A cyclic quadrilateral is a four-sided figure where all vertices lie on the circumference of a circle. One important property of cyclic quadrilaterals is that the sum of the opposite angles is equal to 180∘.
Hint: Remember that in a cyclic quadrilateral, opposite angles add up to 180∘.
Step 2: Identify the given information
We have:
- AB=BC (which means triangle ABC is isosceles)
- AD=DC (which means triangle ADC is also isosceles)
- AC⊥BD (the diagonals are perpendicular)
- ∠CAD=θ
Hint: Write down all the given information clearly to visualize the problem.
Step 3: Analyze triangle ADC
Since AD=DC, the angles opposite these sides are equal. Therefore, we can say:
∠ACD=∠CAD=θ
Hint: Use the property of isosceles triangles to find equal angles.
Step 4: Find angle A+D+C in triangle ADC
The sum of angles in triangle ADC is 180∘:
∠A+∠D+∠C=180∘
Substituting the known angles:
θ+(180∘−2θ)+θ=180∘
This simplifies to:
180∘=180∘
This confirms that our angles are consistent.
Hint: Use the triangle angle sum property to relate the angles.
Step 5: Use the property of cyclic quadrilaterals
Since ABCD is a cyclic quadrilateral, we can use the property that the sum of opposite angles is 180∘:
∠ADC+∠ABC=180∘
Substituting ∠ADC=180∘−2θ:
(180∘−2θ)+∠ABC=180∘
Hint: Set up the equation using the cyclic quadrilateral property.
Step 6: Solve for ∠ABC
Rearranging the equation gives:
∠ABC=2θ
Hint: Isolate ∠ABC to find its value.
Conclusion
Thus, the angle ∠ABC is 2θ.
Final Answer: ∠ABC=2θ
A cyclic quadrilateral is a four-sided figure where all vertices lie on the circumference of a circle. One important property of cyclic quadrilaterals is that the sum of the opposite angles is equal to 180∘.
We have:
- AB=BC (which means triangle ABC is isosceles)
- AD=DC (which means triangle ADC is also isosceles)
- AC⊥BD (the diagonals are perpendicular)
- ∠CAD=θ
Since AD=DC, the angles opposite these sides are equal. Therefore, we can say:
∠ACD=∠CAD=θ
The sum of angles in triangle ADC is 180∘:
∠A+∠D+∠C=180∘
Substituting the known angles:
θ+(180∘−2θ)+θ=180∘
This simplifies to:
180∘=180∘
This confirms that our angles are consistent.
Since ABCD is a cyclic quadrilateral, we can use the property that the sum of opposite angles is 180∘:
∠ADC+∠ABC=180∘
Substituting ∠ADC=180∘−2θ:
(180∘−2θ)+∠ABC=180∘
Rearranging the equation gives:
∠ABC=2θ
Thus, the angle ∠ABC is 2θ.
Similar Questions
Knowledge Check
- Question 1 - Select One
In a cyclic quadrilateral ABCD, AB = BC, AD = DC, AC⊥BD,∠CAD=θ. Then ∠ABC will be-
AθBθ2C2θD3θ - Question 2 - Select One
ABCD is a cyclic trapezium such that AD || BC. If ∠ABC=70∘, then the value of ∠BCD is :
A60∘B70∘C40∘D80∘
A cyclic Quadrilateral ABCD is such that AB=BC, AD=DC and AC and BD intersect at O. If ∠CAD=46∘, then the measure of ∠AOB is equal to:
एक चक्रीय चतुर्भुज ABCD इस प्रकार है की AB = BC, AD = DC और AC और BD पर O पर प्रतिच्छेदित करती है । यदि ∠CAD=46∘ है, तो ∠AOB का माप है: View Solution
View SolutionIn quadrilatcal ABCD, prove that AB+BC+CD+AD<2(BD+AC)
View SolutionIn △ABC, D is a point on AC such that AB = BD = DC. If ∠BAD=70∘, then the measure of ∠B is:
त्रिभुज ABC में, D एक ऐसा बिंदु है कि AB = BD = DC है । यदि ∠BAD=70∘ है, तो कोण B का मान ज्ञात करें |View SolutionABCD is a quadrilateral in which AB=BC and AD =CD ,Show that BD bisects boht the angle ABC and ADC
View SolutionIn quadrilateral ABCD, BA = BC and DA = DC. Prove that BD bisects ∠ ABC as well as ∠ ADC.
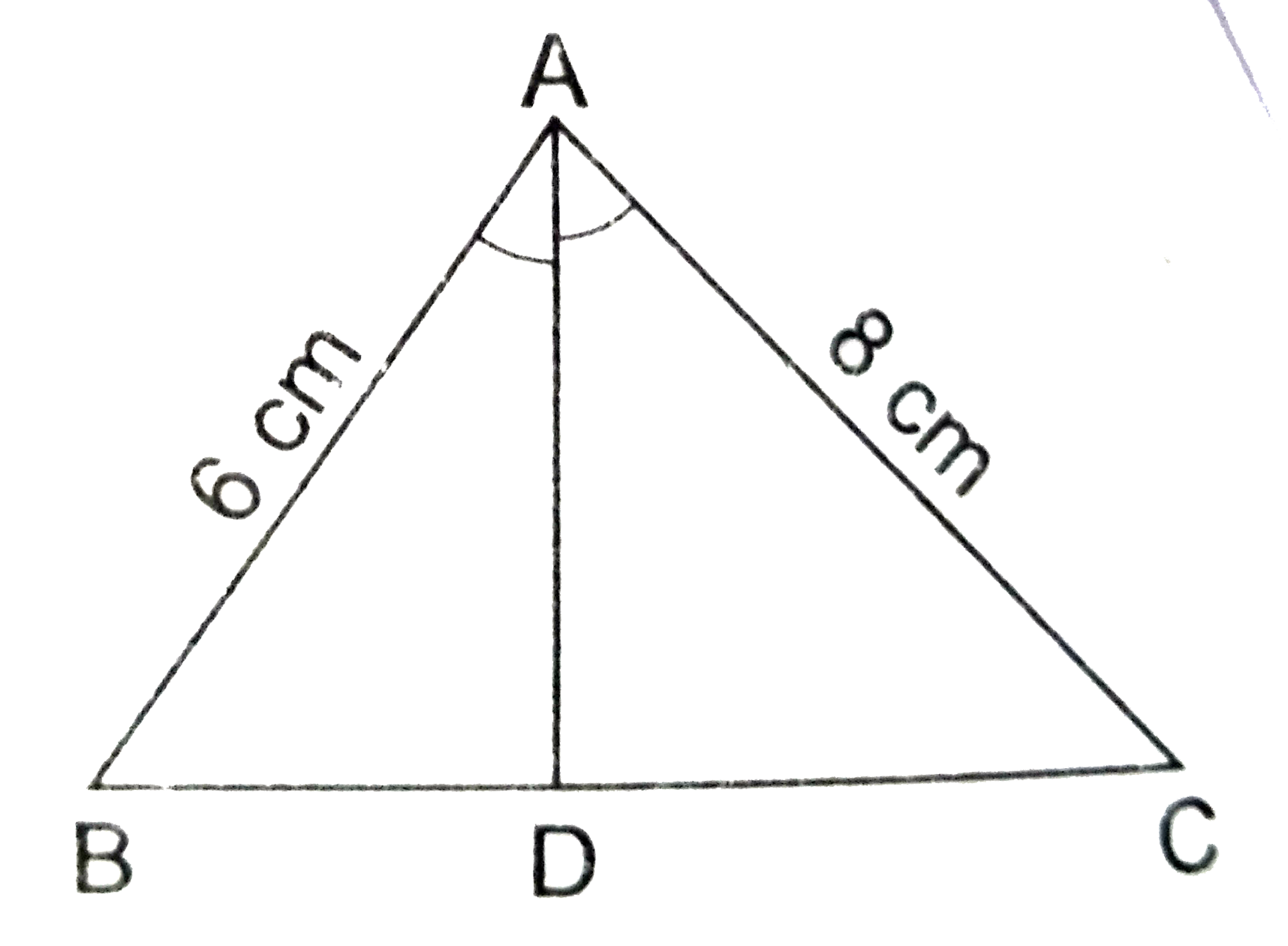
View SolutionIn aΔABC it is given that AB=6cm,AC=8cmandAD is the bisector of ∠A. Then BD:DC=?
 View Solution
View Solution