ABC is a right triangle right-angled at A and AD⊥BC . Then, BDDC= (ABAC)2 (b) ABAC (c) (ABAD)2 (d) ABAD
To solve the problem, we need to analyze the right triangle ABC with A as the right angle and AD being perpendicular to BC. We are required to find the ratio BDDC in terms of the sides of the triangle.
1. Identify the Given Information:
- Triangle ABC is a right triangle with the right angle at A.
- AD is the altitude from A to BC.
2. Understand the Geometry:
- Since AD is perpendicular to BC, we can apply the properties of right triangles and the altitude.
3. Use the Proportionality Theorem:
- The Proportionality Theorem states that if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
- In this case, since AD is perpendicular to BC, we can use the relationship between the segments created by the altitude.
4. Set Up the Ratios:
- According to the theorem, we have:
BDDC=ABAC
- This means that the ratio of the segments BD and DC is equal to the ratio of the sides AB and AC.
5. Conclusion:
- Therefore, we conclude that:
BDDC=ABAC
- This corresponds to option (b) in the choices provided.
Final Answer:
The correct answer is BDDC=ABAC, which is option (b).
- Triangle ABC is a right triangle with the right angle at A.
- AD is the altitude from A to BC.
- Since AD is perpendicular to BC, we can apply the properties of right triangles and the altitude.
- The Proportionality Theorem states that if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
- In this case, since AD is perpendicular to BC, we can use the relationship between the segments created by the altitude.
- According to the theorem, we have:
BDDC=ABAC
- This means that the ratio of the segments BD and DC is equal to the ratio of the sides AB and AC.
- Therefore, we conclude that:
BDDC=ABAC
- This corresponds to option (b) in the choices provided.
The correct answer is BDDC=ABAC, which is option (b).
Topper's Solved these Questions
Similar Questions
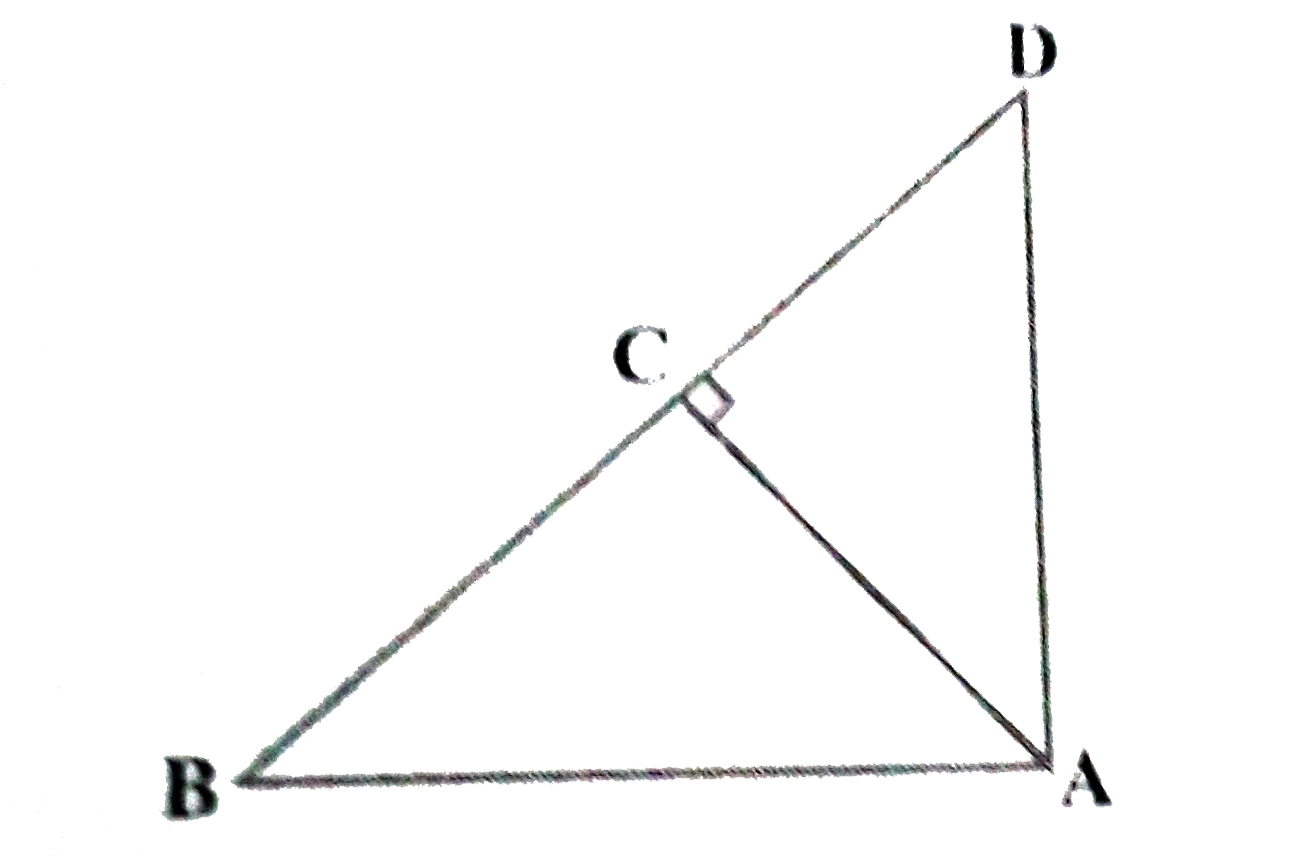
ABD is a right triangle right-angled at A and AC⊥BD . Show that AB2=BC.BD (ii) AC2=BC.DC (iii) AD2=BD.CD (iv) AB2AC2=BDDC
View SolutionIn Figure, ABD is a triangle right-angled at A and AC⊥BD. Show that
(i)AB2=BC.BD
(ii) AC2=BC.DC
(iii) AD2=BD.CD
View SolutionIn a triangle ABC , right angled at B, the inradius is AB+BC−AC2 (b) AB+AC−BC2 AB+BC+AC2 (d) none
View SolutionIn fig.41, ABC is a right triangle right angled at A. D lies on BA produced and DE⊥BC, intersecting AC at F . if ∠AFE=1300, find ∠BDE (ii) ∠BCA ∠ABC
View SolutionIn figure, ABC is a triangle in which ∠ABC=90∘and AD⊥BC. Prove that AC2=AB2+BC2−2BC.BD.

View SolutionIn an equilateral triangle ABC if AD⊥BC, then AD2 = (a)CD2 (b) 2CD2 (c) 3CD2 (d) 4CD2
View SolutionIf in two triangles ABC and DEF , ABDE=BCFE=CAFD , then FDECAB (b) FDEABC (c) CBAFDE (d) BCAFDE
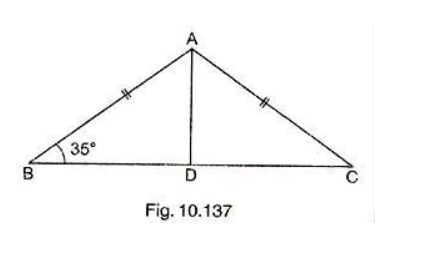
View SolutionABC is an isosceles triangle such that AB=ACandAD is the median to base BC . Then, ∠BAD=
(a) 55∘
(b) 70∘
(c) 35∘
(d) 110∘
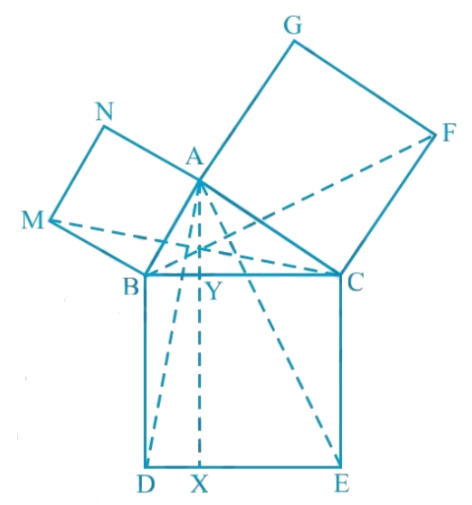
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (BYXD)=2 ar ( MBC)
View SolutionIn Fig. 10.78, if AD, AE and BC are tangents to the circle at D, E and F respectively. Then, (FIGURE) AD=AB+BC+CA (b) 2AD=AB+BC+CA (c) 3AD=AB+BC+CA (d) 4AD=AB+BC+CA
View Solution
