In a circle chords PO and TS are produced to meet at R. If RO 14.4 cm, PO = 11.2 cm and SR = 12.8 cm then the length of chord TS is :
18cm
14.2 cm
12.4 cm
16 cm
The correct Answer is:D
To solve the problem, we will use the intersecting secants theorem, which states that if two secants intersect outside a circle, then the product of the lengths of one secant segment is equal to the product of the lengths of the other secant segment.
1. Identify the Given Values:
- RO = 14.4 cm
- PO = 11.2 cm
- SR = 12.8 cm
- We need to find the length of chord TS.
2. Calculate RP:
- RP is the total length from R to P, which is the sum of RO and PO.
RP=RO+PO=14.4cm+11.2cm=25.6cm
3. Use the Intersecting Secants Theorem:
- According to the theorem:
RO×RP=RS×RT
- We know RO and RP, and we can express RT in terms of TS and SR.
- Let TS = x, then RT = SR + TS = 12.8 cm + x.
4. Set Up the Equation:
- Substitute the known values into the equation:
14.4×25.6=12.8×(12.8+x)
5. Calculate the Left Side:
14.4×25.6=369.84cm2
6. Expand the Right Side:
12.8×(12.8+x)=12.8×12.8+12.8x=163.84+12.8x
7. Set Up the Equation:
369.84=163.84+12.8x
8. Solve for x:
- Subtract 163.84 from both sides:
369.84−163.84=12.8x
206=12.8x
- Divide both sides by 12.8:
x=20612.8=16.09375cm≈16cm
9. Conclusion:
- The length of chord TS is approximately 16 cm.
- RO = 14.4 cm
- PO = 11.2 cm
- SR = 12.8 cm
- We need to find the length of chord TS.
- RP is the total length from R to P, which is the sum of RO and PO.
RP=RO+PO=14.4cm+11.2cm=25.6cm
- According to the theorem:
RO×RP=RS×RT
- We know RO and RP, and we can express RT in terms of TS and SR.
- Let TS = x, then RT = SR + TS = 12.8 cm + x.
- Substitute the known values into the equation:
14.4×25.6=12.8×(12.8+x)
14.4×25.6=369.84cm2
12.8×(12.8+x)=12.8×12.8+12.8x=163.84+12.8x
369.84=163.84+12.8x
- Subtract 163.84 from both sides:
369.84−163.84=12.8x
206=12.8x
- Divide both sides by 12.8:
x=20612.8=16.09375cm≈16cm
- The length of chord TS is approximately 16 cm.
Similar Questions
In a circle, chords PQ and TS are produced to meet at R. If RQ= 14.4 cm, PQ= 11.2 cm and SR=12.8 cm, then the length of chord TS is:
एक वृत्त में, जीवाओं PQ तथा TS को बढ़ाया जाता है जो R पर मिलती हैं | यदि RQ = 14.4 सेमी, PQ =11.2 सेमी तथा SR = 12.8 सेमी है, तो जीवा TS की लंबाई कितनी है ?
View SolutionChords PQ and RS of a circle, when produced, meet at a point O. If PQ = 6cm, OQ = 8cm and OS = 7cm, then length (in cm) of the chord RS is
View Solution
Knowledge Check
In a circle, chords PQ and TS are produced to meet at R. If RQ= 14.4 cm, PQ= 11.2 cm and SR=12.8 cm, then the length of chord TS is:
एक वृत्त में, जीवाओं PQ तथा TS को बढ़ाया जाता है जो R पर मिलती हैं | यदि RQ = 14.4 सेमी, PQ =11.2 सेमी तथा SR = 12.8 सेमी है, तो जीवा TS की लंबाई कितनी है ?A18 cmB16 cmC14.2 cmD112.4 cmChords PQ and RS of a circle, when produced, meet at a point O. If PQ = 6cm, OQ = 8cm and OS = 7cm, then length (in cm) of the chord RS is
A10B12C16D9Two chords AB and CD of a circle are produced to intersect each other at point P outside the circle. If AB=7 cm, BP = 4.2 cm and PD = 2.8 cm, then the length of CD is: /
एक वृत्त की दो जीवाओं AB और CD को बढ़ाया जाता है जो एक-दूसरे को वृत्त के बाहर बिंदु ? पर काटती हैं| यदि AB = 7 सेमी, BP = 4.2 सेमी तथा तथा PD = 2.8 सेमी है, तो CD की लंबाई कितनी है ?A15.8 cmB12 cmC14 cmD14.6 cm
In the given figure,chords AB and CD of a circle intersect externally at P. AB=4 cm,CD=11 cm and PD=15 cm,then the length of PB is:
View SolutionIf the lengths of two parallel chords in a circle of radius 10 cm are 12 cm and 16 cm, then what is the distance between these two chords?
View SolutionA chord AB is drawn in a circle with centre O and radius 5 cm. If the shortest distance between centre and chord is 4 cm, find the length of chord AB?
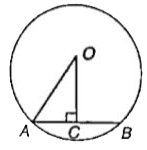
View SolutionIn the given figure, O is the centre of the circle. Radius of the circle is 17 cm. lf OC=8cm, then the length of the chord AB is :
View SolutionIn a circle of radius 17 cm a chord is at a distance of 15 cm form the centre of the circle. What is the length of the chord ?
View Solution
