Let f(x)={−1−2≤x<0x2−10≤x<2 if g(x)=|f(x)|+f(|x|) then g(x) in (−2,2) (A) not continuous (B) not differential at one point (C) differential at all points (D) not differential at two points

A

not differentiable at one point

B

not differentiable at two points

C

differentiable at all points

D

not continuous

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

Key Idea This type of problem can be solved graphically.
We have, f(x)={−1, −2≤x<0x2−1, 0≤x≤2
andg(x)=|f(x)|+f(|x|)
Clearly, |f(x)|={ 1, −2≤x<0∣∣x2−1∣∣, 0≤x≤2
=⎧⎪ ⎪⎨⎪ ⎪⎩ 1, −2≤x<0−(x2−1), 0≤x<1x2−1, 1≤x≤2
and f(|x|)=|x|2−1,0≤|x|≤2
[∵f(|x|)=−1 is not possible as |x|<0]
=x2−1,|x|≤2 [∵|x|2=x2]
=x2−1,−2≤x≤2
∴g(x)=|f(x)|+f(|x|)
=⎧⎪ ⎪⎨⎪ ⎪⎩1+x2−1, −2≤x<0−(x2−1)+x2−1, 0≤x<1x2−1+x2−1, 1≤x≤2
=⎧⎪ ⎪⎨⎪ ⎪⎩x2, −2≤x<00, 0≤x<12(x2−1), 1≤x≤2
Now, let us draw the graph of y= g(x), as shown in the figure.
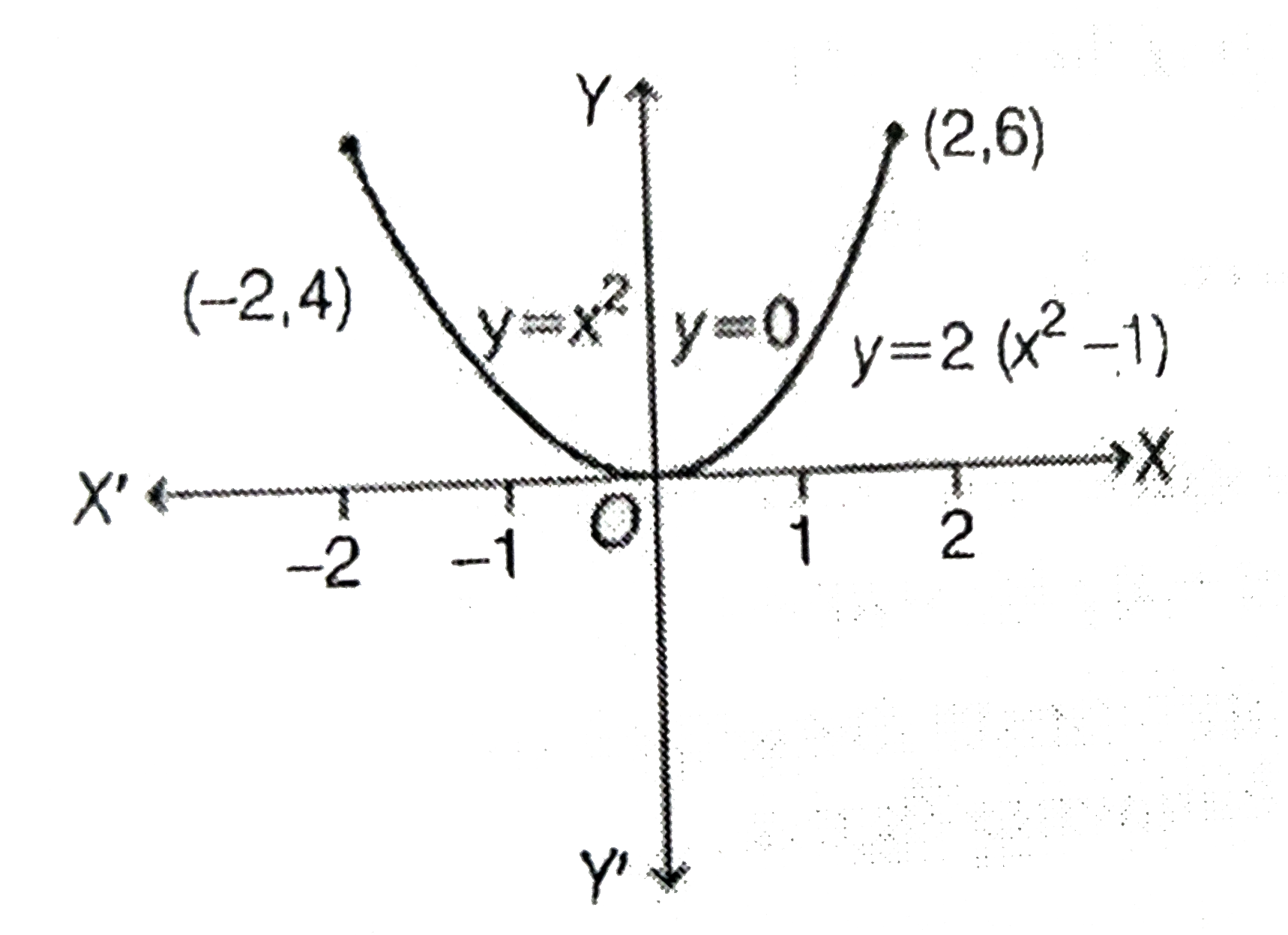
ocr_image
[Here, y=2(x2−1)orx2=12(y+2) represent a parabola with vertex (0, -2) and it open upward]
Note that there is a sharp edge at x = 1 only, so g(x) is not differentiable at x = 1 only.

Updated on:21/07/2023
|
Class 12MATHSLIMITS AND DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Consider f(x)={−2,−1≤x<0x2−2,0≤x≤2 and g(x)=|f(x)|+f(|x|). Then, in the interval (−2,2),g(x) is

    Anot differentiable at one point
    Bdifferentiable at all points
    Cnot continuous
    Dnot differentiable at two points

  • Let f(x)={−1|x|for |x|≥1ax2−bfor |x|<1, If f(x) is continuous and differentiable at any point, then:

    Aa=12,b=−32
    Ba=12,b=32
    Ca=1,b=−1
    Dnone of these

  • Let f(x)=1x2:|x|≥1αx2+β:|x|<1 . If f(x) is continuous and differentiable at any point, then

    Aα=2,β=1
    Bα=−1,β=2
    Cα=1,β=0
    Dα=−2,β=3