Doubtnut Promotions Sticky

let f:R→R be a function defined by f(x)=max{x,x3}. The set of values where f(x) is differentiable is:

A

{−1,1}

B

{−1,0}

C

{0,1}

D

{−1,0,1}

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:D

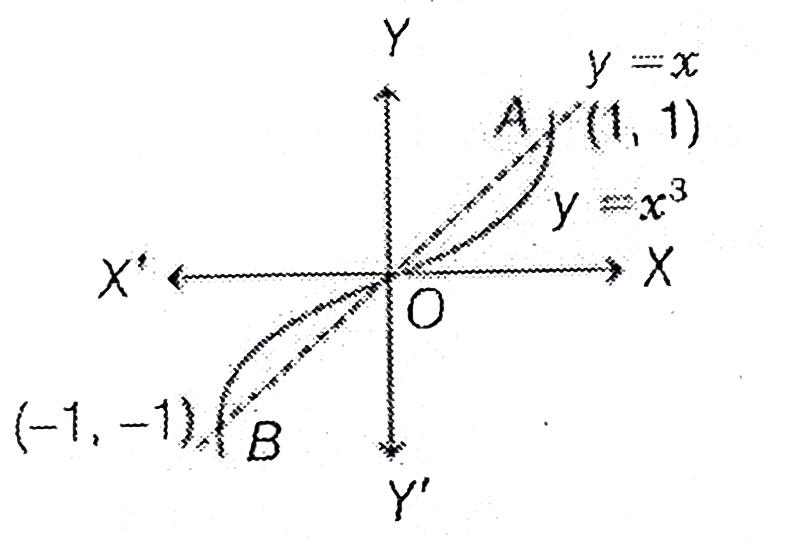
Given, f(x)=max,{x,x3} considering the graph separately, y=x3andy=x
NOTE y=x3 is odd order parabola and y=x is always intersect at (1,1) and (-1,-1).
Now, f(x)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩xin(−∞,−1x3in(−1,0xin(0,1x3in(1,∞
⇒ f(x)=⎧⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪⎩1in(−∞,−13x2in(−1,01in(0,13x2in(1,∞
figure
The point of consideration are
g'(−1−)=1andf'(−1+)=3
f'(−0−)=0andf'(0+)=1
f'(1−)=1andf'(1+)=3
Hence, f is not differentiable at -1,0,1.
ocr_image

|
Updated on:21/07/2023
Class 12MATHSLIMITS AND DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    Let f:R→R be a function defined by f(x)=max.{x,x3}. The set of all points where f(x) is NOT differenctiable is
    (a) {−1,1}
    (b) {−1,0}
    (c ) {0,1}
    (d) {−1,0,1}

    A{−1,1}
    B{−1,0}
    C{0,1}
    D{−1,0,1}
  • Question 2 - Select One

    Let f : R - {n} → R be a function defined by f(x)=x−mx−n, where m≠n. Then,

    Af is one-one and onto
    Bf is one-one and into
    Cf is many-one and onto
    Df is many-one and into