Match the conditions/expressions in Column I with statement in Column Ⅱ. (A). (B)
The correct Answer is:
We know, .
Therefore, . By theory, we know that is differentiable everywhere, therefore .
Again,
Now,
then
which is not differentiable at .
Therefore, is the answer.
Topper's Solved these Questions
- LIMIT,CONTINUITY AND DIFFERENTIABILITY Book:IIT JEE PREVIOUS YEARChapter:LIMIT,CONTINUITY AND DIFFERENTIABILITY Exercise:Differentiability at a point (Fill in the Blanks)
Explore 3 Videos
- LIMIT,CONTINUITY AND DIFFERENTIABILITY Book:IIT JEE PREVIOUS YEARChapter:LIMIT,CONTINUITY AND DIFFERENTIABILITY Exercise:Differentiability at a point (True/False)
Explore 1 Video
- LIMIT,CONTINUITY AND DIFFERENTIABILITY Book:IIT JEE PREVIOUS YEARChapter:LIMIT,CONTINUITY AND DIFFERENTIABILITY Exercise:Differentiability at a point ( Assertion and Reason)
Explore 1 Video
- JEE MAINSBook:IIT JEE PREVIOUS YEARChapter:JEE MAINSExercise:All Questions
Explore 1 Video
- MATRICES AND DETERMINANTSBook:IIT JEE PREVIOUS YEARChapter:MATRICES AND DETERMINANTSExercise:SOLVING SYSTEM OF EQUATIONS (INTEGER ANSWER TYPE QUESTION)
Explore 2 Videos
Similar Questions
Match the conditions/ expressions in Column I with statement in Column II
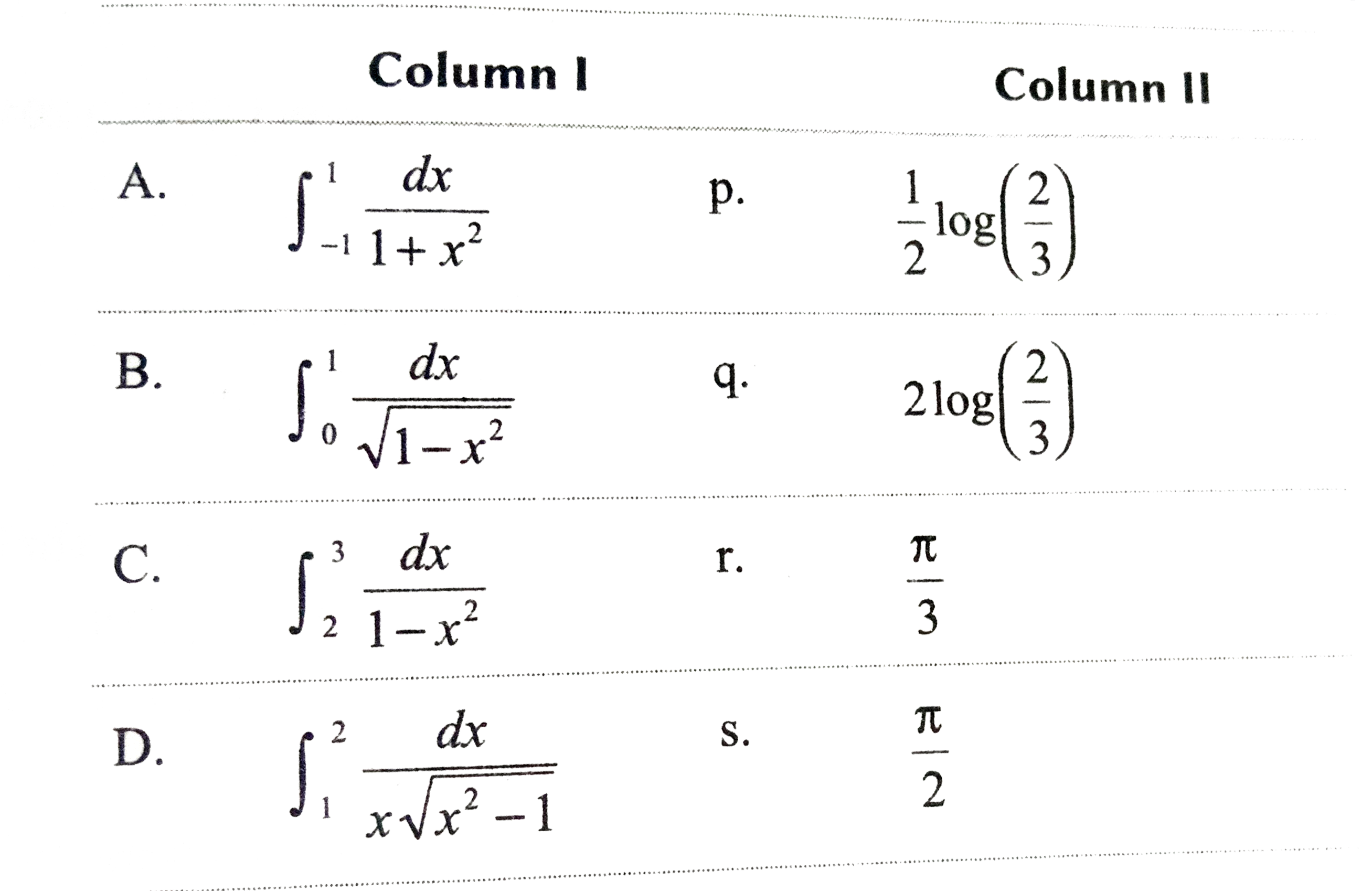
View SolutionMatch the conditions / expression in Column I with statement in Column II.
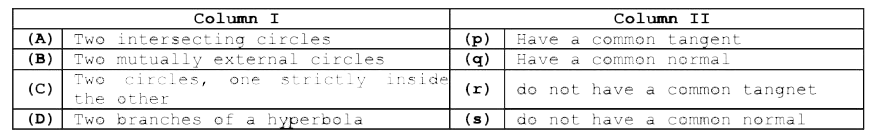
View SolutionMatch the conditions/expressions in Column I with statement in Column Ⅱ. (A). sin(π[x]) (B) sin{π(x−[x])}
View SolutionMatch the conditions /expression n Column I with statement in Column II (z≠0 is a complex number )

View SolutionMatch the ColumnsMatch the conditions/expressions in Column I withstatement in Column II Let f(x)=x2−6x+5x2−5x+6.
View SolutionMatch the conditions/ expressions in Column I with statements in Column II.
Let the functions defined in Column I have domain (−π/2,π/2).
(##41Y_SP_MATH_C10_E02_025_Q01.png" width="80%">
View SolutionMatch the statements/expressions given in Column I with the values given in Column II.

View SolutionMatch the statements/expressions given in Column I with the values given in Column II.

View SolutionMatch the statements/expressions given in Column I with the values given in Column II.

View SolutionMatch the statements/expressions given in Column I with the values given in Column II.

View Solution
