O' is the centre of the circle, AB is a chord of the circle, OM⊥AB. If AB=20cm,OM=2√11 cm, then radius of the circle is
15 cm
12 cm
10 cm
11 cm
The correct Answer is:B
To find the radius of the circle given the chord AB and the perpendicular distance OM from the center O to the chord, we can follow these steps:
1. Identify the Given Information:
- Length of chord AB = 20 cm
- OM (perpendicular distance from the center O to the chord AB) = 2√11 cm
2. Determine the Midpoint of the Chord:
- Since OM is perpendicular to AB, it bisects the chord. Therefore, we can find the lengths of AM and MB.
- Since AB = 20 cm, we have:
AM=MB=AB2=202=10 cm
3. Apply the Pythagorean Theorem:
- In triangle OMA, we can apply the Pythagorean theorem. Here, OA is the radius (r) of the circle, OM is one leg, and AM is the other leg.
- According to the Pythagorean theorem:
OA2=OM2+AM2
4. Substitute the Values:
- Substitute OM and AM into the equation:
OA2=(2√11)2+102
- Calculate OM2 and AM2:
(2√11)2=4×11=44
102=100
- Now, substitute these values back into the equation:
OA2=44+100=144
5. Find the Radius:
- To find OA (the radius), take the square root of both sides:
OA=√144=12 cm
Conclusion:
The radius of the circle is 12 cm.
- Length of chord AB = 20 cm
- OM (perpendicular distance from the center O to the chord AB) = 2√11 cm
- Since OM is perpendicular to AB, it bisects the chord. Therefore, we can find the lengths of AM and MB.
- Since AB = 20 cm, we have:
AM=MB=AB2=202=10 cm
- In triangle OMA, we can apply the Pythagorean theorem. Here, OA is the radius (r) of the circle, OM is one leg, and AM is the other leg.
- According to the Pythagorean theorem:
OA2=OM2+AM2
- Substitute OM and AM into the equation:
OA2=(2√11)2+102
- Calculate OM2 and AM2:
(2√11)2=4×11=44
102=100
- Now, substitute these values back into the equation:
OA2=44+100=144
- To find OA (the radius), take the square root of both sides:
OA=√144=12 cm
The radius of the circle is 12 cm.
Similar Questions
In the given figure, TB is a chord which passes through the centre of the circle. PT is a tangent to the circle at the point T on the circle. If PT = 10 cm, PA = 5 cm and AB = x cm. then the radius of the circle is:
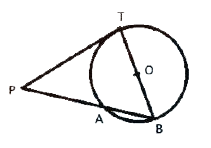 View Solution
View SolutionIn the given figure O is the centre of the circle and AB is a tangent at B. If AB=15 cm and AC=7.5 cm, find the rdius of the circle.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
O is the centre of a circle. AB is a chord of the circle but not its diameter. OC is perpendicular to AB. If OC = CB and radius of the circle be 7 cm, then the length of AB is
A7√2cmB14cmC7 cmD7√2 cm - Question 2 - Select One
In the given figure, TB is a chord which passes through the centre of the circle . PT is a tangent to the circle at the point T on the circle . If PT=10cm, PA=5cm and AB=xcm, then the radius of the circle is :
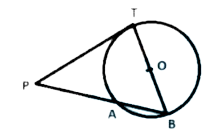 A5√3cmB6√5cmC3√5cmD10√3cm
A5√3cmB6√5cmC3√5cmD10√3cm
AB and CD are parallel chords of a circle 3 cm apart. If AB = 4 cm, CD = 10 cm, then what is the radius of the circle ?
View SolutionPS is the chord of the circle with centre O. A perpendicular is drawn from centre O of the circle to chord PS at M. If ¯¯¯¯¯PS=30cm and ¯¯¯¯¯¯¯OM=8cm, then find the radius of the circle.
View SolutionIf O is the centre of a circle with radius r and AB is a chord of the circle at a distance r2 from O, then ∠BAO=
View SolutionAD is the diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is
View SolutionPS is the chord of the circle with centre O. A perpendicular is drawn from centre O of the circle to chord PS at M. If ¯¯¯¯¯PS=30cm and ¯¯¯¯¯¯¯OM=8cm, then find the radius of the circle.
View SolutionIn the figure above, O is the centre of the circle CD is a tangent to the circle at E. OE bisects the chord AB at F. AB = 16 cm and EF = 2 cm. Find the length of DE (in cm).
 View Solution
View Solution

