AD is the diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is
17 cm
15 cm
13 cm
8 cm
To find the distance of the chord AB from the center of the circle, we can follow these steps:
Step 1: Identify the radius of the circle
Since AD is the diameter of the circle, we can find the radius by dividing the diameter by 2.
- Given: AD = 34 cm
- Radius (r) = AD / 2 = 34 cm / 2 = 17 cm
Hint: Remember that the radius is half the length of the diameter.
Step 2: Draw a perpendicular from the center to the chord
Let O be the center of the circle, and let the perpendicular from O to the chord AB meet AB at point M. By properties of circles, this perpendicular bisects the chord.
Hint: The perpendicular from the center of a circle to a chord bisects the chord.
Step 3: Find the length of AM
Since AB is bisected by OM, we can find the lengths of AM and MB.
- Given: AB = 30 cm
- Therefore, AM = AB / 2 = 30 cm / 2 = 15 cm
Hint: When a chord is bisected, each segment is equal in length.
Step 4: Apply the Pythagorean theorem
In the right triangle OMA, we can apply the Pythagorean theorem to find the distance OM (the distance from the center to the chord).
- We know:
- OA (the radius) = 17 cm
- AM (half the chord) = 15 cm
- OM (the distance from the center to the chord) = ?
Using the Pythagorean theorem:
OA2=OM2+AM2
172=OM2+152
Step 5: Calculate OM
Substituting the values:
289=OM2+225
OM2=289−225
OM2=64
OM=√64
OM=8 cm
Final Answer
The distance of the chord AB from the center of the circle is 8 cm.
---
Since AD is the diameter of the circle, we can find the radius by dividing the diameter by 2.
- Given: AD = 34 cm
- Radius (r) = AD / 2 = 34 cm / 2 = 17 cm
Let O be the center of the circle, and let the perpendicular from O to the chord AB meet AB at point M. By properties of circles, this perpendicular bisects the chord.
Since AB is bisected by OM, we can find the lengths of AM and MB.
- Given: AB = 30 cm
- Therefore, AM = AB / 2 = 30 cm / 2 = 15 cm
In the right triangle OMA, we can apply the Pythagorean theorem to find the distance OM (the distance from the center to the chord).
- We know:
- OA (the radius) = 17 cm
- AM (half the chord) = 15 cm
- OM (the distance from the center to the chord) = ?
OA2=OM2+AM2
172=OM2+152
Substituting the values:
289=OM2+225
OM2=289−225
OM2=64
OM=√64
OM=8 cm
The distance of the chord AB from the center of the circle is 8 cm.
Similar Questions
In the adjoining figure, O is the centre of the centre of the circle. If diameter AC=26cm and chord AB=10cm, then find the distances of the chord AB from the centre of the circle.
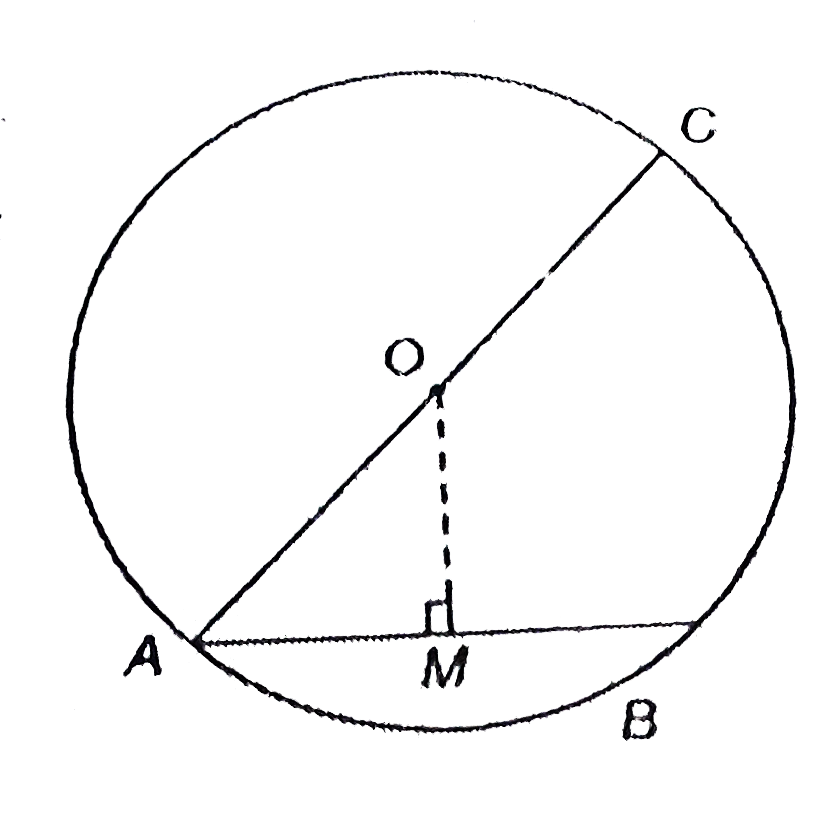
View SolutionAB is a chord of a circle with centre O and diameter 20 cm. If AB = 12 cm, find the distance of AB from O.
View Solution
Knowledge Check
AD is a diameter of a circle and AB is a chord. If AD = 34cm, AB = 30cm, the distance of AB form the centre of the circle is
A17 cmB15 cmC4 cmD8 cmIn the adjoining figure, O is the centre of circle and diameter AC=26cm. If chord AB=10cm, then the distance between chord AB and centre O of the circle is :
 A24 cmB16 cmC12 cmDnone of the above
A24 cmB16 cmC12 cmDnone of the aboveA chord 6 cm long is at a distance of 4 cm from the centre of a circle. Find the length of a chord which is at a distance of 3 cm from the centre of the circle.
A10 cmB6 cmC8 cmD12 cm
AB and CD are parallel chords of a circle 3 cm apart. If AB = 4 cm, CD = 10 cm, then what is the radius of the circle ?
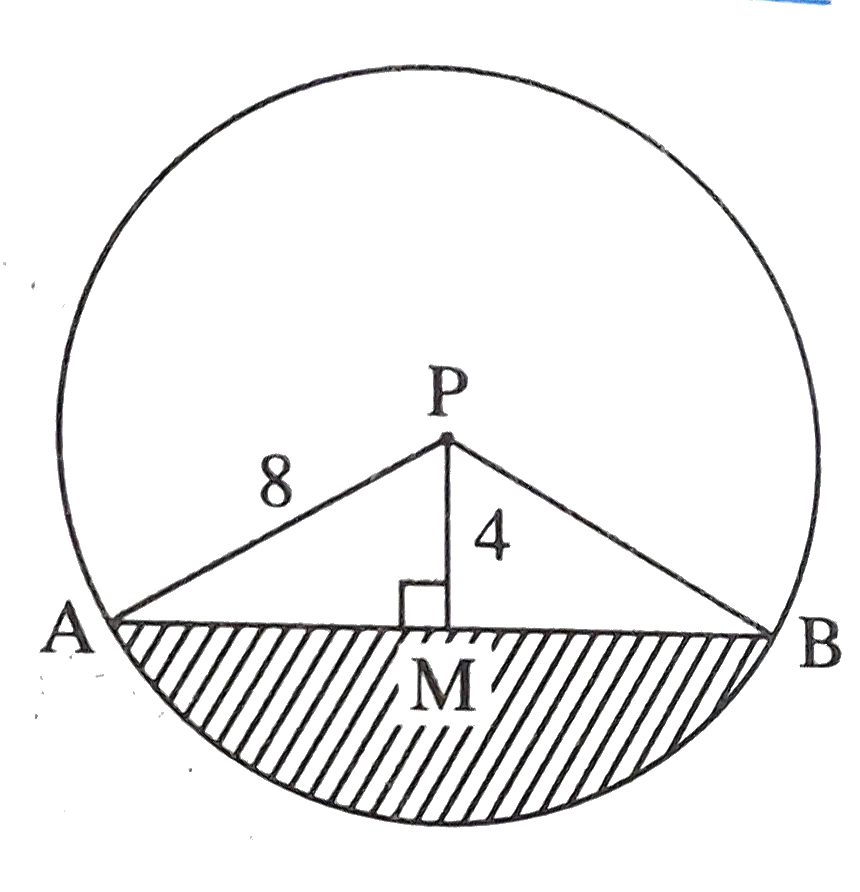
View SolutionIn the figure, seg AB is a chord of a circle with centre P. If PA = 8 cm and distance of chord AB from the centre P is 4 cm, find the area of the shaded portion.
View SolutionO' is the centre of the circle, AB is a chord of the circle, OM⊥AB. If AB=20cm,OM=2√11 cm, then radius of the circle is
View SolutionIn a class of 39 students the ratio of boys and girls is 2 : 1. Radhika ranks 15th among all the students from top and 8th among girls from bottom. How many boys are there below Radhika ?
View SolutionThe length of a chord of a circle at a distance of 5 cm from the centre is 24 cm. The diameter of the circle is
View Solution
