X and Y are two loops made from same wire. The radii of X and Y are r1 and r2 and their M.I are I1 and I2 . If I2/I1=4 the value of r2r1 is (K)1/3. Find the value of K.
To solve the problem, we need to find the value of K given that the moment of inertia ratio I2I1=4 and the relationship r2r1=K1/3.
1. Understand the Moment of Inertia: The moment of inertia I of a loop (ring) is given by the formula:
I=mr2
where m is the mass of the loop and r is its radius.
2. Express the Mass: Since both loops X and Y are made from the same wire, their masses can be expressed in terms of their radii. The mass m of a loop can be calculated as:
m=ρ×Volume
For a thin wire loop, the volume can be approximated as the cross-sectional area multiplied by the circumference. Thus, the mass of loop X (with radius r1) and loop Y (with radius r2) can be expressed as:
m1=ρ⋅2πr1⋅tandm2=ρ⋅2πr2⋅t
where t is the thickness of the wire and ρ is the density of the material.
3. Substitute Mass into Moment of Inertia: Now substituting m1 and m2 into the moment of inertia formulas:
I1=m1r21=(ρ⋅2πr1⋅t)r21=ρ⋅2πt⋅r31
I2=m2r22=(ρ⋅2πr2⋅t)r22=ρ⋅2πt⋅r32
4. Set Up the Ratio: Now, we can set up the ratio of the moments of inertia:
I2I1=ρ⋅2πt⋅r32ρ⋅2πt⋅r31=r32r31
Given that I2I1=4, we can write:
r32r31=4
5. Relate the Radii: Taking the cube root of both sides gives:
r2r1=41/3
6. Express in Terms of K: From the problem, we have r2r1=K1/3. Therefore, we can equate:
K1/3=41/3
7. Find K: Cubing both sides results in:
K=4
Final Answer
The value of K is 4.
I=mr2
where m is the mass of the loop and r is its radius.
m=ρ×Volume
For a thin wire loop, the volume can be approximated as the cross-sectional area multiplied by the circumference. Thus, the mass of loop X (with radius r1) and loop Y (with radius r2) can be expressed as:
m1=ρ⋅2πr1⋅tandm2=ρ⋅2πr2⋅t
where t is the thickness of the wire and ρ is the density of the material.
I1=m1r21=(ρ⋅2πr1⋅t)r21=ρ⋅2πt⋅r31
I2=m2r22=(ρ⋅2πr2⋅t)r22=ρ⋅2πt⋅r32
I2I1=ρ⋅2πt⋅r32ρ⋅2πt⋅r31=r32r31
Given that I2I1=4, we can write:
r32r31=4
r2r1=41/3
K1/3=41/3
K=4
The value of K is 4.
Topper's Solved these Questions
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER -7 (GRAVITATION)
15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER -7 (MECHANICAL PROPERTIES OF SOLIDS)
15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER -5 (WORK, ENERGY AND POWER)
15 Videos
- ATOMSBOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-2: CONCEPT APPLICATOR
30 Videos
- COMMUNICATION SYSTEM BOOK - DISHA PUBLICATIONCHAPTER - COMMUNICATION SYSTEM EXERCISE - EXERCISE-2 : Concept Applicator
30 Videos
Similar Questions
Knowledge Check
Two loops P and Q are made from a uniform wire. The redii of P and Q are r1andr2 respectively, and their moments of inertia are I1andI2 respectively, IfI2=4I1,thenr2r1equals-
A42/3B41/3C4−2/3D4−1/3Two loops P and Q are made from a uniform wire. The redii of P and Q are r1andr2 respectively, and their moments of inertia are I1andI2 respectively, IfI2=4I1,thenr2r1equals-
A423B413C4−23D4−13Two loops P and Q are made from a uniform wire. The redii of P and Q are r1andr2 respectively, and their moments of inertia are I1andI2 respectively, IfI2=4I1,thenr2r1equals-
A42/3B41/3C4−2/3D4−1/3
The magnitude of gratitational field intensities at distance r1 and r2 from the centre of a uniform solid sphere of radius R and mass M are I1 and I2 respectively. Find the ratio of I1/I2 if (a) r1>R and r2>R and (b) r1<R and r2<R (c ) r1>R and r2<R.
View SolutionTwo loops P and Q are made from a uniform wire. The radii of P and Q are R1andR2 respectively and their moments of inertia are IPandIQ respectively.
If IPIQ=8 then R1R2 is
View SolutionTwo loops P and Q are made from a uniform wire. The radii of P and Q are R1 and R2, respectively, and their moments of inertia about their axis of rotation are I1 and I2, respectively. If I1I2=4, then R2R1 is
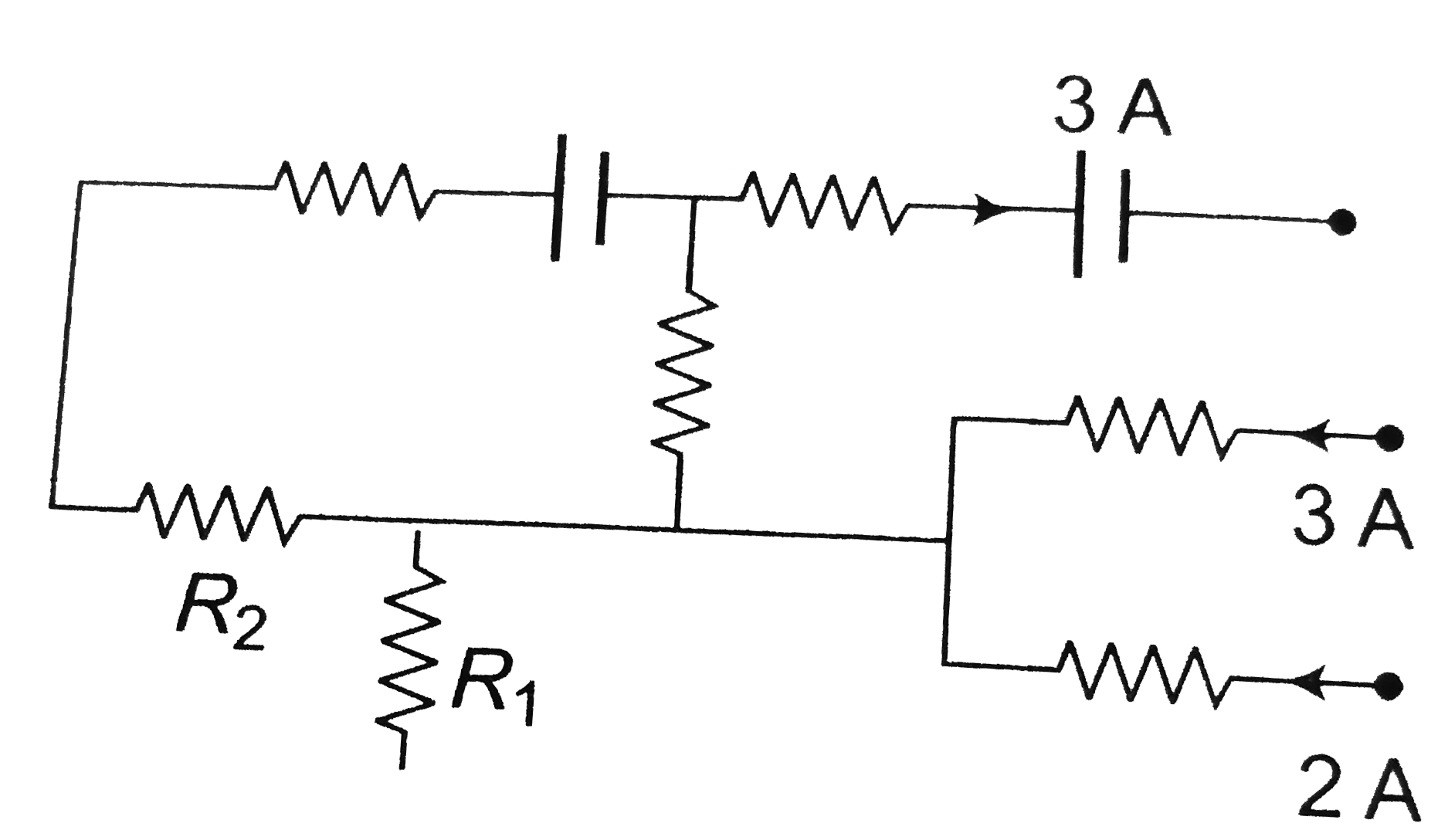
View SolutionIn the given circuit if I1 and I2 be the current in resistance R1 and R2 respectively then:
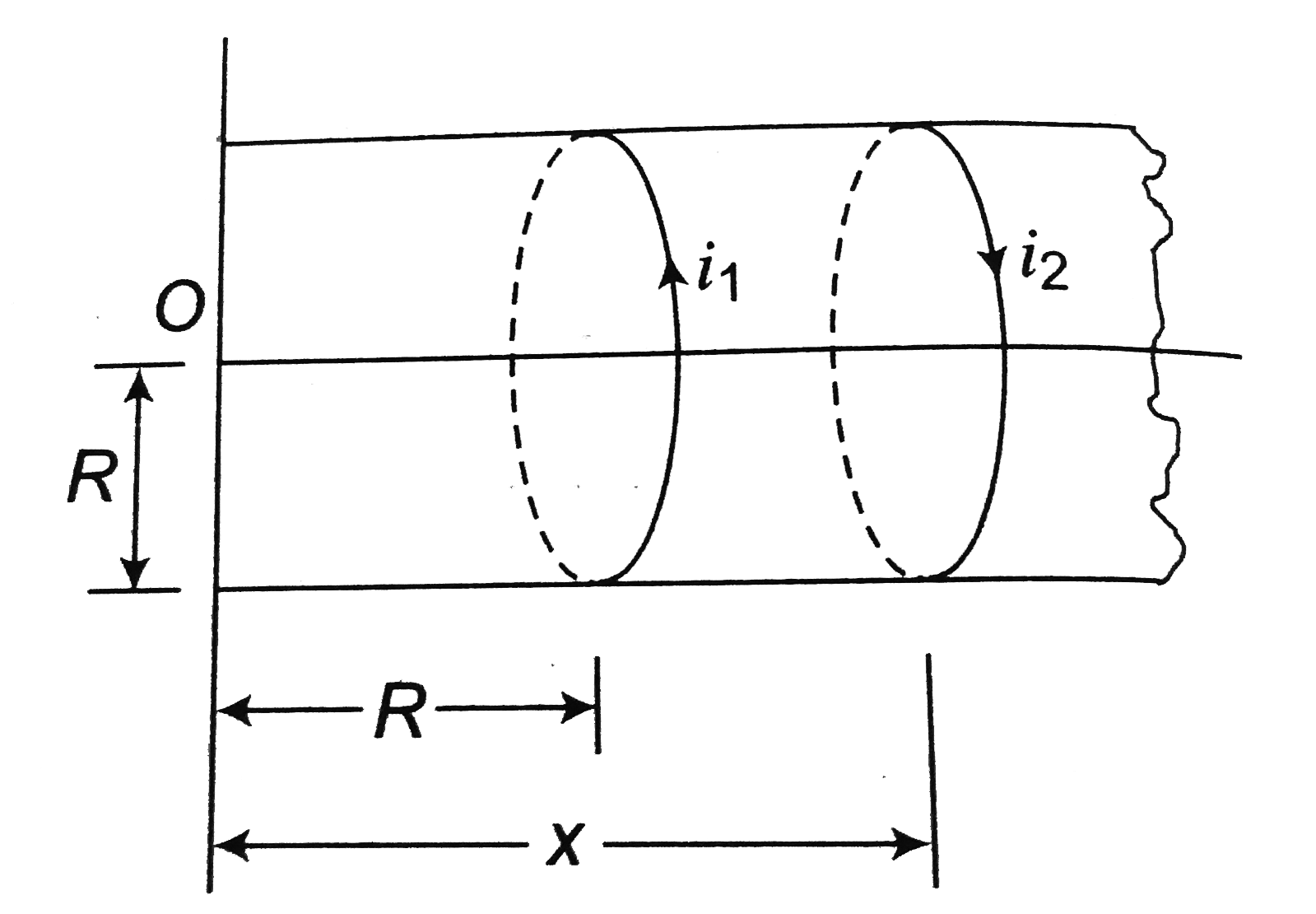
View SolutionTwo wires are wrapped over wooden cylinder to form two co-axial loops carrying currents i1 and i2. If i2=8i1 the value of x for B=0 at the origin O is:
View Solution
