A rigid bar of mass 15 kg is supported symmetrically by three wires each 2 m long. Those at each end are of copper and middle one is of iron. Determine the ratio of their diameters if each is to have the same tension. Young's modulus of elasticity for copper and steel are and respectively.
Each wire has same tension soa eah wire wil have same extension. Also as they have same lengt, each wire will have same strain
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER-9 (MECHANICAL PROPERTIES OF FLUIDS)15videos
CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONS
- BOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER -10 (THERMAL PROPERTIES OF MATTER)15videos
CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONS
- BOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER -7 (GRAVITATION)15videos
CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONS
- BOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-2: CONCEPT APPLICATOR30videos
ATOMS
- BOOK - DISHA PUBLICATIONCHAPTER - COMMUNICATION SYSTEM EXERCISE - EXERCISE-2 : Concept Applicator30videos
COMMUNICATION SYSTEM
Similar Questions
A rigid bar of mass 15 kg is supported symmetrically by three wires each 2 m long. Those at each end aer of copper and middle one is of iron. Determine the ratio of their diameters if each is to have the same tensoin. Young's modulus of elasticity for copper and steel are 110×109Nm−2 and 190×109Nm−2 respectively.
View SolutionA block of weight 100 N is suspended by copper and steel wires of same cross sectional area 0.5cm2 and, length √3 m and 1m, respectively. Their other ends are fixed on a ceiling as shown in figure. The angles subtended by copper and steel wires with ceiling are 30∘and60∘, respectively. If elongation in copper wire is (ΔlC) and elongation in steel wire is (Δls), then the ratio ΔlCΔls is -
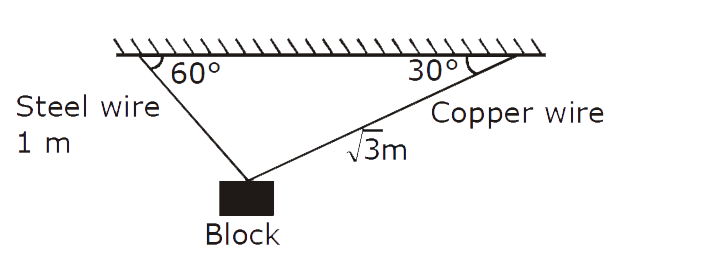
[Young's modulus for copper and steel are 1×1011N/m2and2×1011N/m2, respectively]View Solution
Knowledge Check
- Question 1 - Select One
A rigid bar of mass M is supported symmetrically by three wires each of length l. Those at each end are of copper and the middle one is of iron. The ratio of their diameters, if each is to have the same tension, is equal to
AYcopper/YironB√YironYcopperCY2ironY2copperDYironYcopper - Question 2 - Select One
A rigid bar of mass M is supported symmetrically by three wires each of length l. Those at each end are of copper and the middle one is of ion. The ratio of their diameters, if each is to have the same tension, is equal to
AYcopper/YironB√YironYcopperCY2ironY2copperDYironYcopper - Question 3 - Select One
A rigid bar of mass M is supported symmetrically by three wires each of length l. Those at each end are of copper and the middle one is of iron. The ratio of their diameters, if each is to have the same tension, is equal to
AYcopperYironB√YironYcopperCY2ironY2copperDYironYcopper
Choose the most appropriate option.
A rigid bar of mass 15 kg is supported symmetrically by three wires each 2 m long. Those at each end are of copper and the middle one is of iron. Determine the ratio of their diameters if each is to have the tension.View SolutionA rigid bar of mass M is supported symmetrically by three wires each of length I. Those at each end are of copper and the middle one is of iron. What is the ratio of their diameters DcopperDiron if each wire is to have ratio same tension?
View SolutionA rigid bar of mass 15 kg is supported symmetrically by three wires, each of length 2 m. The wires at the endpoints are made of copper and the middle one is made of steel. If the tension in each wire is the same, then the diameter of copper wire to the diameter of steel wire is [Given, Ycopper=1.1×1011N m−2andYsteel=1.9×1011N m−2]
View SolutionSteel and copper wires of same length are stretched by the same weight one after the other. Young's modulus of steel and copper are 2×1011Nm2 and 1.2×1011Nm2. The ratio of increase in length is
View SolutionIf a wire of length 4 m and cross-sectional area of 2 m2 is stretched by a force of 3 kN, then determine the change in length due to this force, Given, Young's modulus of material of wire is 110×109Nm−2
View Solution

