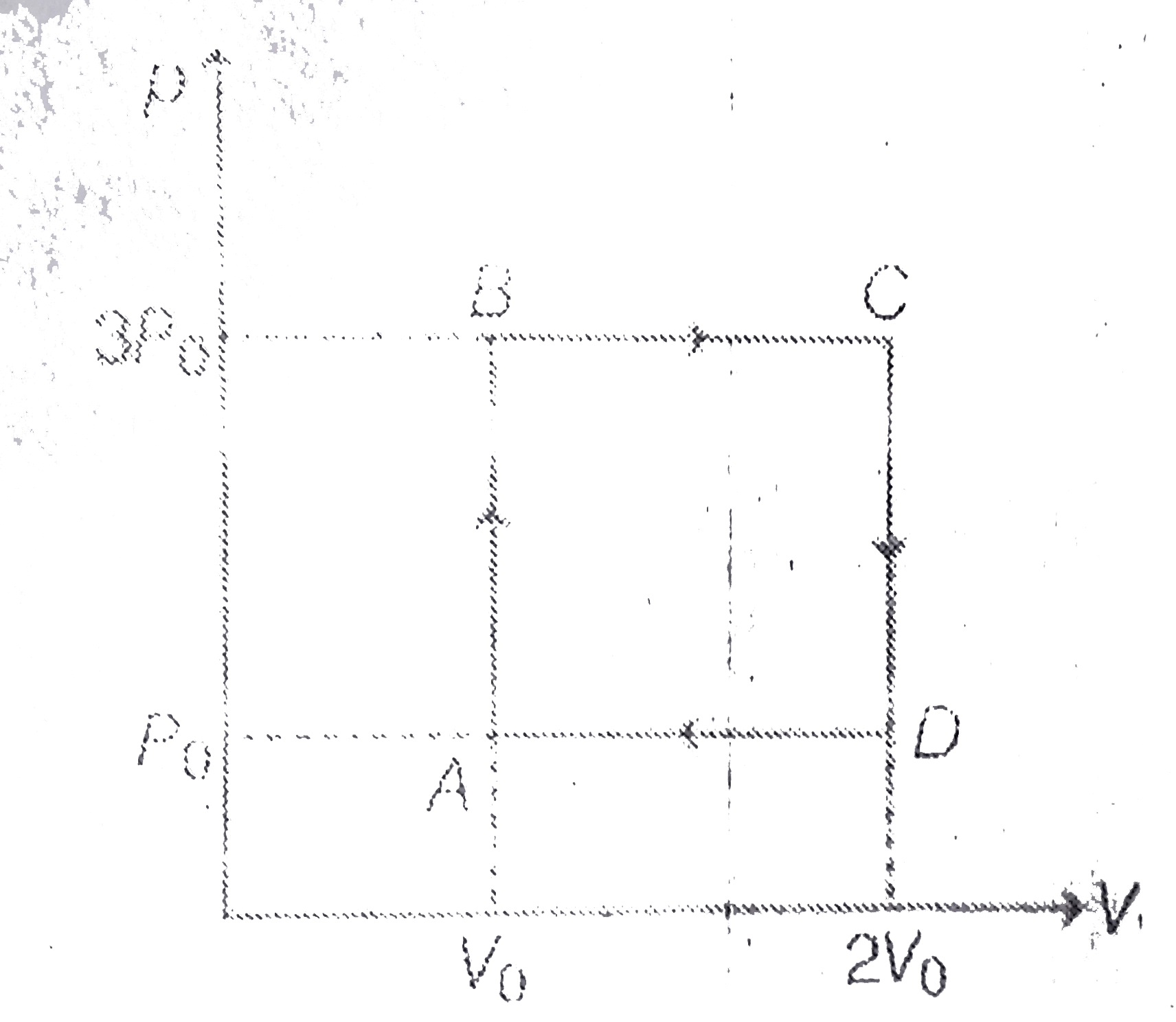
Helium gas goes through a cycle ABCDA (consisting of two isochoric and isobaric lines) as shown in figure. Find efficienty of this cycle. (Assume the gas to be close to an ideal gas)

Text Solution

Verified by Experts

If $T_{0}$ be the temperature at A then temperature at B,

$\frac{P_{0} V_{0}}{T_{0}} = \frac{2 P_{0} \times V_{0}}{T_{B}}$ or $T_{B} = 2 T_{0}$
And temperature at C becomes $4 T_{0}$
Heat is extracted by the system in process $A \to B$ and $B \to C$
so
$Q = Q_{v} + Q_{P}$
$= n C V D e < A T = n L C_{P} Δ T$
$= n \times \frac{3 R}{2} \times (2 T_{0} - T_{0}) + n \times \frac{5 R}{2} (4 T_{0} - 2 T_{0})$
$= \frac{13}{2} n R T_{0}$
Work done in the complete cycle
$W = P_{0} V_{0} = n R T_{0}$
Now efficiency $η = \frac{W}{Q}$
$= \frac{n R T_{0}}{\frac{13}{2} n R T_{0}} \times 100$
$= 15.4 %$

Updated on:21/07/2023